
分析 (1)根据万有引力提供向心力,万有引力等于重力,结合卫星的周期大小,求出卫星的轨道半径,从而得出卫星离地的高度.
(2)根据万有引力等于重力得出星球的质量,结合星球的体积得出密度的表达式,结合地球和月球的半径之比、表面的重力加速度之比求出密度之比.
解答 解:(1)由题意知,“嫦娥三号”卫星的周期为 T=$\frac{t}{n}$,
设卫星离月球表面的高度为h,由万有引力提供向心力得:
$G\frac{Mm}{({R}_{0}+h)^{2}}=m({R}_{0}+h)\frac{4{π}^{2}}{{T}^{2}}$,
月球表面质量为m1的物体受到的重力等于月球的引力,
$G\frac{M{m}_{1}}{{{R}_{0}}^{2}}={m}_{1}{g}_{0}$,
解得h=$\root{3}{\frac{{g}_{0}{{R}_{0}}^{2}{t}^{2}}{4{π}^{2}{n}^{2}}}-{R}_{0}$.
(2)质量为m2的物体,在地球和月球表面受到的重力等于各中心天体的引力
$G\frac{M{m}_{2}}{{R}^{2}}={m}_{2}g$,
M=ρV,
又V=$\frac{4π{R}^{3}}{3}$,
解得$ρ=\frac{3g}{4πGR}$,
可知$\frac{{ρ}_{地}}{{ρ}_{月}}=\frac{\frac{3{g}_{地}}{4πG{R}_{地}}}{\frac{3{g}_{月}}{4πG{R}_{月}}}=\frac{{g}_{地}{R}_{月}}{{g}_{月}{R}_{地}}$,
代入数据,$\frac{{R}_{月}}{{R}_{地}}=\frac{1}{4}$,$\frac{{g}_{地}}{{g}_{月}}=6$,
解得:$\frac{{ρ}_{地}}{{ρ}_{月}}=\frac{3}{2}$.
答:(1)“嫦娥三号”卫星离月球表面高度为$\root{3}{\frac{{g}_{0}{{R}_{0}}^{2}{t}^{2}}{4{π}^{2}{n}^{2}}}-{R}_{0}$.
(2)地球和月球的密度之比为3:2.
点评 解决本题的关键掌握万有引力定律的两个重要理论:1、万有引力等于重力,2、万有引力提供向心力,并能灵活运用.


科目:高中物理 来源: 题型:选择题
| A. | 大黑洞质量可表达为$\frac{4{π}^{2}{r}^{3}}{G{T}^{2}}$ | |
| B. | 若黑洞间引力不断增强,则小黑洞的周期将大于T | |
| C. | 若黑洞间引力不断增强,则小黑洞的向心加速度将变小 | |
| D. | 大黑洞质量为太阳质量的$\frac{{r}^{3}}{{r}_{0}^{3}{T}^{2}}$倍 |
查看答案和解析>>
科目:高中物理 来源: 题型:解答题
 如图,在水平匀强电场中,固定一个半径为,的绝缘细管,管内光滑,管面水平(管横截面的半径远小于r),匀强电场的场强大小为E,方向与直径AB平行,在管的圆心O处放置一个电荷量为+Q的点电荷.假设另有一个带电荷量为+q、质量为m的小球,恰好能在管内完成圆周运动,求
如图,在水平匀强电场中,固定一个半径为,的绝缘细管,管内光滑,管面水平(管横截面的半径远小于r),匀强电场的场强大小为E,方向与直径AB平行,在管的圆心O处放置一个电荷量为+Q的点电荷.假设另有一个带电荷量为+q、质量为m的小球,恰好能在管内完成圆周运动,求查看答案和解析>>
科目:高中物理 来源: 题型:填空题
查看答案和解析>>
科目:高中物理 来源: 题型:解答题
 “嫦娥三号”探测器成功实施近月制动,顺利进入环月轨道,并在月球成功地进行了一系列研究.为人类征服太空奠定基础,“嫦娥四号”择日发射,若把探测器环月运行轨道可视为圆轨道,忽略地球及其他天体的引力对探测器的影响,设探测器环月运行轨道半径为r,月球半径为R,运行周期为T,引力常量为G,求:
“嫦娥三号”探测器成功实施近月制动,顺利进入环月轨道,并在月球成功地进行了一系列研究.为人类征服太空奠定基础,“嫦娥四号”择日发射,若把探测器环月运行轨道可视为圆轨道,忽略地球及其他天体的引力对探测器的影响,设探测器环月运行轨道半径为r,月球半径为R,运行周期为T,引力常量为G,求:查看答案和解析>>
科目:高中物理 来源: 题型:多选题
| A. | $(\frac{2π}{T})^{2}nR$ | B. | ($\frac{2π}{T}$)2R | C. | $\frac{g}{{n}^{2}}$ | D. | $\frac{g}{n}$ |
查看答案和解析>>
科目:高中物理 来源: 题型:多选题
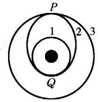 如图所示,发射地球同步卫星时,先将卫星发射至近地圆轨道1,然后经点火,使其沿椭圆轨道2运行,最后再次点火,将卫星送入同步轨道3.轨道1、2相切于Q点,轨道2、3相切于P点(如图所示),则当卫星分别在1、2、3轨道正常运行时,以下说法正确的是( )
如图所示,发射地球同步卫星时,先将卫星发射至近地圆轨道1,然后经点火,使其沿椭圆轨道2运行,最后再次点火,将卫星送入同步轨道3.轨道1、2相切于Q点,轨道2、3相切于P点(如图所示),则当卫星分别在1、2、3轨道正常运行时,以下说法正确的是( )| A. | 卫星在轨道3上的速度大于在轨道1上的速度 | |
| B. | 卫星在轨道3上的角速度小于在轨道1上的角速率 | |
| C. | 卫星在轨道2上经过Q点时的速度大于它在轨道2上经过P点时的速度 | |
| D. | 卫星在轨道1上经过Q点时的加速度小于它在轨道2上经过Q点时的加速度 |
查看答案和解析>>
科目:高中物理 来源: 题型:多选题
| A. | 地球的向心力变为缩小前的一半 | |
| B. | 地球的向心力变为缩小前的$\frac{1}{16}$ | |
| C. | 地球绕太阳公转周期变为缩小前的$\frac{1}{4}$ | |
| D. | 地球绕太阳公转周期不变 |
查看答案和解析>>
科目:高中物理 来源: 题型:填空题
 某同学利用图所示的装置,通过半径相同且质量分别为m1、m2的A、B两球所发生的碰撞来验证动量守恒定律.图中o点为球离开轨道时球心的投影位置,p点为A球单独平抛后的落点,p1、p2分别为A、B碰撞后A、B两球的落点.已知A球始终从同一高度滚下.今测得op=x,op1=x1,op2=x2,则动量守恒表达式为m1•x=m1•x1+m2•x2,(用m1、m2、x1、x2表示)若表达式m1•x2=m1•x12+m2•x22成立,则可判断AB发生弹性正碰.
某同学利用图所示的装置,通过半径相同且质量分别为m1、m2的A、B两球所发生的碰撞来验证动量守恒定律.图中o点为球离开轨道时球心的投影位置,p点为A球单独平抛后的落点,p1、p2分别为A、B碰撞后A、B两球的落点.已知A球始终从同一高度滚下.今测得op=x,op1=x1,op2=x2,则动量守恒表达式为m1•x=m1•x1+m2•x2,(用m1、m2、x1、x2表示)若表达式m1•x2=m1•x12+m2•x22成立,则可判断AB发生弹性正碰.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com