
| A. | 地球绕太阳运行的周期及地球离太阳的距离 | |
| B. | 人造地球卫星在地面附近运行的周期和轨道半径 | |
| C. | 若不考虑地球自转,已知地球的半径及地球表面的重力加速度 | |
| D. | 月球绕地球运行的周期及月球的半径 |
分析 地球、月球、人造卫星等做匀速圆周运动,它们受到的万有引力充当向心力,用它们的运动周期表示向心力,由万有引力定律结合牛顿第二定律列式求中心天体的质量,然后由选项条件判断正确的答案.
解答 解:A、地球绕太阳运动的周期和地球与太阳的距离,根据万有引力提供向心力:$G\frac{Mm}{{r}^{2}}=m\frac{4{π}^{2}}{{T}^{2}}r$,其中m为地球质量,在等式中消去,只能求出太阳的质量M.也就是说只能求出中心体的质量.故A错误.
B、人造卫星绕地球做匀速圆周运动,它受到地球的万有引力充当向心力,用它运动周期表示向心力,
由万有引力定律结合牛顿第二定律得:$G\frac{Mm}{{r}^{2}}=m\frac{4{π}^{2}}{{T}^{2}}r$,又因T=$\frac{2π}{ω}$,所以地球的质量M=$\frac{T{v}^{3}}{2πG}$,因此,可求出地球的质量,故B正确.
C、地球表面的物体受到的地球的重力等于万有引力,即mg=G$\frac{Mm}{{r}^{2}}$,因此,可求出地球的质量M=$\frac{{r}^{2}g}{G}$,故C正确.
D、月球绕地球做匀速圆周运动,它受到地球的万有引力充当向心力,用它运动周期表示向心力,由万有引力定律结合牛顿第二定律得:$G\frac{Mm}{{r}^{2}}=m\frac{4{π}^{2}}{{T}^{2}}r$,所以地球的质量M=$\frac{4{π}^{2}{r}^{3}}{G{T}^{2}}$,其中r为地球与月球间的距离,而不是月球的半径,故D错误.
故选:BC.
点评 解答万有引力定律在天体运动中的应用时要明确天体做匀速圆周运动,其受到的万有引力提供向心力,会用线速度、角速度、周期表示向心力,同时注意公式间的化简.


科目:高中物理 来源: 题型:多选题
| A. | 当沿运动方向油滴间距逐渐增大时,小四轮做加速直线运动 | |
| B. | 当沿运动方向油滴始终均匀分布时,小四轮做匀速直线运动 | |
| C. | 当沿运动方向油滴间距逐渐增大时,车的加速度可能在减小 | |
| D. | 当沿运动方向油滴间距逐渐增大时,车的加速度可能在增大 |
查看答案和解析>>
科目:高中物理 来源: 题型:解答题
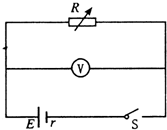 如图所示,R为电阻箱,V为理想电压表.当电阻箱读数为R1=2Ω时,电压表读数为 U1=3V;当电阻箱读数为R2=4Ω时,电压表读数为U2=4V.求:
如图所示,R为电阻箱,V为理想电压表.当电阻箱读数为R1=2Ω时,电压表读数为 U1=3V;当电阻箱读数为R2=4Ω时,电压表读数为U2=4V.求:查看答案和解析>>
科目:高中物理 来源: 题型:解答题
查看答案和解析>>
科目:高中物理 来源: 题型:选择题
| A. | g值随高度的增加而增大 | |
| B. | g值在地面任何地方都一样 | |
| C. | g值在赤道处大于南北两极处 | |
| D. | 同一地点轻重不同的物体的g值一样大 |
查看答案和解析>>
科目:高中物理 来源: 题型:多选题
| A. | 氧气的内能较大 | B. | 氢气的内能较大 | ||
| C. | 二者内能相等 | D. | 氢气分子的平均速率较大 |
查看答案和解析>>
科目:高中物理 来源: 题型:选择题
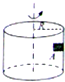 如图所示,一半径为R的圆筒绕中心轴匀速转动.圆筒侧壁的小木块A能随圆筒一起做匀速圆周运动,则木块A受力的个数为( )
如图所示,一半径为R的圆筒绕中心轴匀速转动.圆筒侧壁的小木块A能随圆筒一起做匀速圆周运动,则木块A受力的个数为( )| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com