
 (2012?肇庆二模)如图所示,带电平行金属板PQ和MN之间的距离为d;两金属板之间有垂直纸面向里的匀强磁场,磁感应强度大小为B.建立如图所示的坐标系,x轴平行于金属板,且与金属板中心线重合,y轴垂直于金属板.区域I的左边界是y轴,右边界与区域II的左边界重合,且与y轴平行;区域II的左、右边界平行.在区域I和区域II内分别存在匀强磁场,磁感应强度大小均为B,区域I内的磁场垂直于Oxy平面向外,区域II内的磁场垂直于Oxy平面向里.一电子沿着x轴正向以速度v0射入平行板之间,在平行板间恰好沿着x轴正向做直线运动,并先后通过区域I和II.已知电子电量为e,质量为m,区域I和区域II沿x轴方向宽度均为
(2012?肇庆二模)如图所示,带电平行金属板PQ和MN之间的距离为d;两金属板之间有垂直纸面向里的匀强磁场,磁感应强度大小为B.建立如图所示的坐标系,x轴平行于金属板,且与金属板中心线重合,y轴垂直于金属板.区域I的左边界是y轴,右边界与区域II的左边界重合,且与y轴平行;区域II的左、右边界平行.在区域I和区域II内分别存在匀强磁场,磁感应强度大小均为B,区域I内的磁场垂直于Oxy平面向外,区域II内的磁场垂直于Oxy平面向里.一电子沿着x轴正向以速度v0射入平行板之间,在平行板间恰好沿着x轴正向做直线运动,并先后通过区域I和II.已知电子电量为e,质量为m,区域I和区域II沿x轴方向宽度均为
| ||
| 2Be |
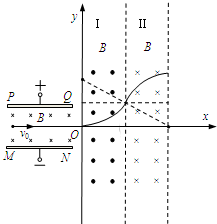 解:(1)电子在平行板间做直线运动,电场力与洛伦兹力平衡,
解:(1)电子在平行板间做直线运动,电场力与洛伦兹力平衡,| U |
| d |
| ||
| R |
| ||
| 2Be |
| mv0 |
| 2eB |
| mv0 |
| eB |
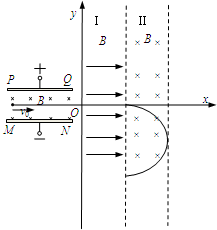
| v2 |
| r |
| ||
| 2 |
. |
| v |
| v0+v |
| 2 |
| b | ||
|
| ||
| 2Be |
| 3 |
| m |
| eB |
| v2 |
| r |
| 2πr |
| T |
| T |
| 2 |
| πm |
| eB |
| πm |
| eB |
| 3 |
| m |
| eB |
| 5m |
| eB |
| mv0 |
| eB |
| 5m |
| eB |


 暑假作业安徽少年儿童出版社系列答案
暑假作业安徽少年儿童出版社系列答案湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com