
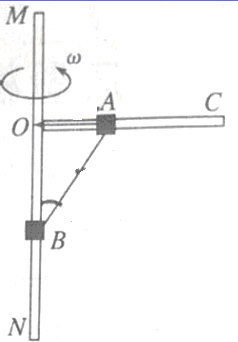
 如图所示,光滑圆杆MN段竖直,OC段水平且与MN相接于O点,两杆分别套有质量为m的环A和质量为2m的环B,两环的内径比杆的直径稍大,A、B用长为2L的轻绳连接,A和O点用长为L的轻绳连接,现让装置绕竖直杆MN做匀速圆周运动,当ω=$\sqrt{\frac{2g}{L}}$时,OA段绳刚好要断,AB段绳能承受的拉力足够大,求:
如图所示,光滑圆杆MN段竖直,OC段水平且与MN相接于O点,两杆分别套有质量为m的环A和质量为2m的环B,两环的内径比杆的直径稍大,A、B用长为2L的轻绳连接,A和O点用长为L的轻绳连接,现让装置绕竖直杆MN做匀速圆周运动,当ω=$\sqrt{\frac{2g}{L}}$时,OA段绳刚好要断,AB段绳能承受的拉力足够大,求:分析 (1)OA段绳子刚刚拉直时,拉力为零,对B分析,AB绳子竖直方向上的分力等于B的重力,水平方向的分力提供A做圆周运动的向心力,根据牛顿第二定律求出此时的角速度.
(2)根据OA绳恰好拉断时的角速度,结合牛顿第二定律求出最大拉力.
(3)转动稳定时,AB绳竖直方向的分力等于B的重力,水平方向的分力提供A做圆周运动的向心力,根据牛顿第二定律求出绳子与竖直方向的夹角,结合几何关系求出A向外侧移动的距离.
解答 解:(1)当OA段绳刚刚拉直时,对B分析,在竖直方向上有:
TABcosθ=2mg,
${T}_{AB}sinθ=mL{{ω}_{1}}^{2}$,
解得:${ω}_{1}=\sqrt{\frac{2\sqrt{3}g}{3L}}$.
(2)根据牛顿第二定律得:
${T}_{m}+{T}_{AB}sinθ=mL{ω}^{2}$,
解得:Tm=$\frac{6-2\sqrt{3}}{3}mg$.
(3)当ω=$\sqrt{\frac{3g}{L}}$且转动稳定时,设绳子与竖直方向的夹角为α,
则TAB′cosα=2mg,${T}_{AB}′sinα=m2Lsinα{ω}^{2}$,
代入数据解得:$cosα=\frac{1}{3}$,
则有:sinα=$\frac{2\sqrt{2}}{3}$,
A向外侧移动的距离为:$△x=2L×\frac{2\sqrt{2}}{3}-L=\frac{4\sqrt{2}-3}{3}L$.
答:(1)OA段绳子刚刚拉直时转动的角速度为$\sqrt{\frac{2\sqrt{3}g}{3L}}$;
(2)OA段绳能承受的最大拉力为$\frac{6-2\sqrt{3}}{3}mg$;
(3)当ω=$\sqrt{\frac{3g}{L}}$且转动稳定时,A向外侧移动的距离为$\frac{4\sqrt{2}-3}{3}L$.
点评 解决本题的关键知道A物体做圆周运动向心力的来源,抓住临界状态,结合牛顿第二定律进行求解.


科目:高中物理 来源: 题型:解答题
查看答案和解析>>
科目:高中物理 来源: 题型:解答题
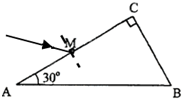 如图所示,一棱镜的截面为直角三角形ABN,∠A=30°,斜面AB=a,在此截面所在的平面内,一条光线以45°的入射角从AN边的中点M左侧射入棱镜,已知棱镜材料的折射率为n=$\sqrt{2}$.
如图所示,一棱镜的截面为直角三角形ABN,∠A=30°,斜面AB=a,在此截面所在的平面内,一条光线以45°的入射角从AN边的中点M左侧射入棱镜,已知棱镜材料的折射率为n=$\sqrt{2}$.查看答案和解析>>
科目:高中物理 来源: 题型:选择题
| A. | 该行星的密度 | B. | 该行星的自转周期 | ||
| C. | 该星球的第一宇宙速度 | D. | 该行星附近运行的卫星的最小周期 |
查看答案和解析>>
科目:高中物理 来源: 题型:填空题

查看答案和解析>>
科目:高中物理 来源: 题型:选择题
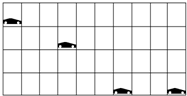 做杂技表演的汽车从高台水平飞出,在空中运动后着地,一架照相机通过多次曝光,拍摄得到汽车在着地前后一段时间内的运动照片,并且汽车刚好到达地面时拍到一次.如图所示,已知汽车长度为3.6m,相邻两次曝光时间间隔相等,由照片(图中实线是用笔画的正方形的格子)可推算出汽车离开高台时的瞬时速度大小和高台离地面高度分别为(g取10m/s2)( )
做杂技表演的汽车从高台水平飞出,在空中运动后着地,一架照相机通过多次曝光,拍摄得到汽车在着地前后一段时间内的运动照片,并且汽车刚好到达地面时拍到一次.如图所示,已知汽车长度为3.6m,相邻两次曝光时间间隔相等,由照片(图中实线是用笔画的正方形的格子)可推算出汽车离开高台时的瞬时速度大小和高台离地面高度分别为(g取10m/s2)( )| A. | 18m/s;11.25 m | B. | 18m/s;7.2m | C. | 12m/s;11.25m | D. | 12m/s;7.2 m |
查看答案和解析>>
科目:高中物理 来源: 题型:填空题
查看答案和解析>>
科目:高中物理 来源: 题型:选择题
 如图所示,A、B两物块叠放在一起,在光滑的水平面上保持相对静止地向右做匀速直线运动,运动过程中B受到的摩擦力( )
如图所示,A、B两物块叠放在一起,在光滑的水平面上保持相对静止地向右做匀速直线运动,运动过程中B受到的摩擦力( )| A. | 方向向左,大小不变 | B. | 方向向左,逐渐减小 | ||
| C. | 方向向右,大小不变 | D. | 不受摩擦力 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com