
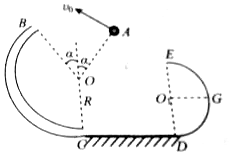
 如图所示,O为竖直放置的半径R=2m的光滑管状轨道圆心,A、B两点关于O的竖直线对称,从A点将质量为m=0.2kg的小球以某一速度斜向上抛出,无碰撞地由B点进入管道,小球经圆轨道最低点C无能量损失地进入长L=4m水平粗糙轨道CD,小球与CD间动摩擦因数μ=0.2,光滑半圆轨道DE竖直放置,E为最高点,G是与圆心O1等高的点,小球经D点无能量损失进入半圆轨道并能到达EG间某处,已知圆管的直径远小于轨道半径R且略大于小球直径,OB与竖直方向间夹角α=37°,(取sin37°=0.6,g取10m/s2)求:
如图所示,O为竖直放置的半径R=2m的光滑管状轨道圆心,A、B两点关于O的竖直线对称,从A点将质量为m=0.2kg的小球以某一速度斜向上抛出,无碰撞地由B点进入管道,小球经圆轨道最低点C无能量损失地进入长L=4m水平粗糙轨道CD,小球与CD间动摩擦因数μ=0.2,光滑半圆轨道DE竖直放置,E为最高点,G是与圆心O1等高的点,小球经D点无能量损失进入半圆轨道并能到达EG间某处,已知圆管的直径远小于轨道半径R且略大于小球直径,OB与竖直方向间夹角α=37°,(取sin37°=0.6,g取10m/s2)求:分析 (1)根据斜抛运动的对称性以及小球无碰撞地由B点进入管道,说明小球在A点的初速度与OA垂直,运用运动的分解法和分位移公式列式,可求得小球过B点时的速度vB;
(2)小球恰能过E点,由重力提供向心力,由牛顿第二定律求得E点的速度.小球从D到E,运用机械能守恒定律求出小球到达D点时的速度.在D点,根据牛顿定律求小球在D点时对轨道的压力;
(3)根据小球恰好到达E点和G点的临界条件以及机械能守恒定律分别列式,可求得r的范围.
解答 解:(1)因为A、B关于过O点的竖直线对称且小球能无碰撞地由B点进入管道,所以小球在A点的初速度与OA垂直,设小球到达B点时竖直分速度为vy,水平速度为vx.从A到B的时间为t,则由斜抛运动规律知:
2Rsinα=vxt
vy=g•$\frac{t}{2}$
且 tanα=$\frac{{v}_{y}}{{v}_{x}}$
联立并代入数据解得 vx=4m/s,vy=3m/s
故小球过B点时的速度 vB=$\sqrt{{v}_{x}^{2}+{v}_{y}^{2}}$=5m/s
(2)小球恰能过E点时,有 mg=m$\frac{{v}_{E}^{2}}{r}$
小球从D到E,由机械能守恒定律得
2mgr+$\frac{1}{2}m{v}_{E}^{2}$=$\frac{1}{2}m{v}_{D}^{2}$
在D点,由牛顿第二定律得
FN-mg=m$\frac{{v}_{D}^{2}}{r}$
联立解得 FN=6mg=6×0.2×10N=12N
由牛顿第三定律知,小球在D点时对轨道的压力为12N.
(3)小球从B到D的过程,由动能定理得
mgR(1+cosα)-μmgL=$\frac{1}{2}m{v}_{D}^{2}$-$\frac{1}{2}m{v}_{B}^{2}$
解得 vD=9m/s
当小球刚能过G点时,由机械能守恒定律得:
$\frac{1}{2}m{v}_{D}^{2}$=mgrmax,解得 rmax=4.05m
当小球恰能到E点时,有:
$\frac{1}{2}m{v}_{D}^{2}$=2mgrmin+$\frac{1}{2}m{v}_{E}^{2}$
在E点有 mg=m$\frac{{v}_{E}^{2}}{{r}_{min}}$
解得 rmin=1.62m
所以半圆轨道DE的半径r应满足的条件是 1.62m<r<4.05m
答:
(1)小球过B点时的速度vB是5m/s.
(2)若小球恰能过E点,则小球在D点时对轨道的压力是12N;
(3)半圆轨道DE的半径r应满足的条件是 1.62m<r<4.05m.
点评 解决本题的关键要理解斜抛运动的对称性,明确圆周运动的临界条件,知道小球刚到E点时由重力充当向心力.


科目:高中物理 来源: 题型:计算题
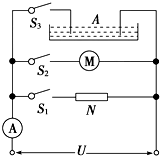 如图所示,A为电解槽,M为电动机,N为电炉子,恒定电压U=12V,电解槽内阻rA=2Ω,当S1闭合、S2、S3断开时,电流表A示数为6A;当S2闭合、S1、S3断开时,A示数为5A,且电动机输出功率为35W;当S3闭合、S1、S2断开时,A示数为4A.求:
如图所示,A为电解槽,M为电动机,N为电炉子,恒定电压U=12V,电解槽内阻rA=2Ω,当S1闭合、S2、S3断开时,电流表A示数为6A;当S2闭合、S1、S3断开时,A示数为5A,且电动机输出功率为35W;当S3闭合、S1、S2断开时,A示数为4A.求:查看答案和解析>>
科目:高中物理 来源: 题型:选择题
| A. | 时刻表示时间极短,时间表示时间较长 | |
| B. | 2min只能分成120个时刻 | |
| C. | 作息时间表上的数字均表示时间 | |
| D. | 在时间轴上,时刻对应的是一个点,时间对应的是一段 |
查看答案和解析>>
科目:高中物理 来源: 题型:解答题
查看答案和解析>>
科目:高中物理 来源: 题型:计算题
 质量为1500kg 的汽车在平直的公路上运动,v-t图象如图所示.由此求:
质量为1500kg 的汽车在平直的公路上运动,v-t图象如图所示.由此求:查看答案和解析>>
科目:高中物理 来源: 题型:多选题
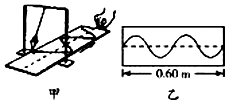 图甲是利用沙摆演示简谐运动的装置,当盛沙的漏斗下面的薄木板被水平匀速拉出时,做简谐运动的漏斗漏出的沙在板上显示出图乙所示的曲线.已知木板水平速度为0.20m/s,图乙所示一段木板的长度为0.60m,取g=π2,则( )
图甲是利用沙摆演示简谐运动的装置,当盛沙的漏斗下面的薄木板被水平匀速拉出时,做简谐运动的漏斗漏出的沙在板上显示出图乙所示的曲线.已知木板水平速度为0.20m/s,图乙所示一段木板的长度为0.60m,取g=π2,则( )| A. | 沙摆的摆长大约为0.56 m | B. | 沙摆的摆长大约为1.00 m | ||
| C. | 图乙可表示沙摆的振动图象 | D. | 图乙可表示沙摆的波动图象 |
查看答案和解析>>
科目:高中物理 来源: 题型:选择题
| A. | 质点在过A点后1s内的位移时5m | |
| B. | 质点在过A点前1s内的位移时5m | |
| C. | 若质点从A点开始做匀速直线运动,则以后每1s内的位移都是5m | |
| D. | 质点在以过A点时刻为中间时刻的1s内的位移一定是5m |
查看答案和解析>>
科目:高中物理 来源: 题型:多选题
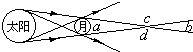
| A. | 位于区域a、b内的人可看到月全蚀 | B. | 位于区域c、d内的人可看到日全蚀 | ||
| C. | 位于区域b内的人可看到日环蚀 | D. | 位于区域c、d内的人可看到日偏蚀 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com