
 如图,在直角坐标系xOy中,点M(0,l)处不断向抄方向发射出大量质量为m、带电量为-q的粒子(不计粒子重力),粒子的初速度大小广泛分布于零到v0之间.已知这些粒子此后所经磁场区域的磁感应强度大小均相同,方向垂直于纸面向里,其中0≤x≤l区域内的磁场分布如图所示(即虚线MP下方无磁场),l≤x≤2l区域无磁场,2l≤x≤3l区域的磁场分布未画出.己知所有粒子都沿+x方向经过,0≤x≤2l区域,且都沿-y的方向通过点N(3l,0),其中速度大小为v0的粒子刚好从P点通过.则:
如图,在直角坐标系xOy中,点M(0,l)处不断向抄方向发射出大量质量为m、带电量为-q的粒子(不计粒子重力),粒子的初速度大小广泛分布于零到v0之间.已知这些粒子此后所经磁场区域的磁感应强度大小均相同,方向垂直于纸面向里,其中0≤x≤l区域内的磁场分布如图所示(即虚线MP下方无磁场),l≤x≤2l区域无磁场,2l≤x≤3l区域的磁场分布未画出.己知所有粒子都沿+x方向经过,0≤x≤2l区域,且都沿-y的方向通过点N(3l,0),其中速度大小为v0的粒子刚好从P点通过.则:分析 (1)在0-l区域,速度为v0的粒子偏转90°后从P离开磁场,求出圆周运动的半径,根据半径公式求解B;
(2)带电粒子沿y轴正方向射入,在磁场的洛伦兹力作用下发生偏转,然后所以粒子沿+x方向经过b区域,则磁场的右边界由数学关系推导出与R无关,而是一条直线.那么磁场的左边界则是一段圆弧,其半径由洛伦兹力提供向心力公式求解得.由于对称,则可求出磁场的最小面积.
(3)两种粒子在磁场中运动时间是相等,它们发射的时间差是因速度不同导致的.
解答  解:(1)在0-l区域,速度为v0的粒子偏转90°后从P离开磁场,则:
解:(1)在0-l区域,速度为v0的粒子偏转90°后从P离开磁场,则:
r=l=$\frac{m{v}_{0}}{Bq}$
解得:B=$\frac{m{v}_{0}}{lq}$
(2)此后粒子均沿+x方向穿过l-2l区域,进入2l-3l区域,
由对称性可知,其磁场区域如图,磁场面积最小,最小面积为S=$\frac{1}{4}π{l}^{2}-\frac{1}{2}{l}^{2}$
(3)速度为αv0的粒子在磁场中做匀速圆周运动的时间t=${t}_{1}+{t}_{2}=2×\frac{πm}{2Bq}=\frac{πm}{Bq}$,则该段时间与粒子速度无关,
而速度为αv0的粒子在没有磁场区域做匀速直线运动的时间$t′=\frac{2(l-R)+l}{α{v}_{0}}+\frac{l}{{αv}_{0}}=\frac{4l-2R}{α{v}_{0}}$,其中R为速度为αv0的粒子做圆周运动的半径,
且R=$\frac{mα{v}_{0}}{Bq}=αl$,所以$t′=\frac{(4-2α)l}{α{v}_{0}}$,
同理速度为βv0的粒子做匀速直线运动的时间为$t″=\frac{(4-2β)l}{β{v}_{0}}$
所以这两个粒子的发射时间差$△t=t″-t′=\frac{4l}{{v}_{0}}(\frac{1}{β}-\frac{1}{α})$.
答:(1)磁场的磁感应强度B为$\frac{m{v}_{0}}{lq}$;
(2)2l≤x≤3l区域内符合要求的磁场范围的最小面积为$\frac{1}{4}π{l}^{2}-\frac{1}{2}{l}^{2}$;
(3)若其中速度为αv0和βv0的两个粒子同时到达N点(0<β<α<1),则二者发射的时间差△t为$\frac{4l}{{v}_{0}}(\frac{1}{β}-\frac{1}{α})$.
点评 利用数学表达式,导出磁场右边界的函数关系式.同时相同粒子不同速度在磁场中的时间是相等,由于速度的不同,导致直线运动中时间不一.


 阅读快车系列答案
阅读快车系列答案科目:高中物理 来源: 题型:选择题
| A. | 将没切线方向做匀速直线运动飞出 | B. | 将做靠近圆心的曲线运动 | ||
| C. | 做远离圆心的曲线运动 | D. | 将做平抛运动 |
查看答案和解析>>
科目:高中物理 来源: 题型:解答题
 如图所示,在宽为L=0.5m的平行导轨上垂直导轨放置一个有效电阻为r=0.6Ω的直导体棒,在导轨的两端分别连接两个电阻R1=4Ω、R2=6Ω,其他电阻不计.整个装置处在垂直导轨向里的匀强磁场中,磁感应强度B=0.1T.当直导体棒在导轨上以v=6m/s的速度向右运动时,求:
如图所示,在宽为L=0.5m的平行导轨上垂直导轨放置一个有效电阻为r=0.6Ω的直导体棒,在导轨的两端分别连接两个电阻R1=4Ω、R2=6Ω,其他电阻不计.整个装置处在垂直导轨向里的匀强磁场中,磁感应强度B=0.1T.当直导体棒在导轨上以v=6m/s的速度向右运动时,求:查看答案和解析>>
科目:高中物理 来源: 题型:选择题
 如图所示,正方形区域abcd中充满匀强磁场,磁场的方向垂直纸面向里.n,m、n′、m′分别是各边的中点.一个氢核从m点沿着既垂直于ad边又垂直于磁场的方向,以一定速度射入磁场,正好从n点射出磁场.若将磁场的磁感应强度变为原来的2倍,磁场的方向改为垂直纸面向外,其他条件则不交,则这个氢核射出磁场的位置是( )
如图所示,正方形区域abcd中充满匀强磁场,磁场的方向垂直纸面向里.n,m、n′、m′分别是各边的中点.一个氢核从m点沿着既垂直于ad边又垂直于磁场的方向,以一定速度射入磁场,正好从n点射出磁场.若将磁场的磁感应强度变为原来的2倍,磁场的方向改为垂直纸面向外,其他条件则不交,则这个氢核射出磁场的位置是( )| A. | 在d、n′之间的某点 | B. | 在n、a之间的某点 | ||
| C. | 在d、m之间的某点 | D. | 在d点 |
查看答案和解析>>
科目:高中物理 来源: 题型:解答题
| U/V | 1.40 | 1.20 | 1.00 | 0.70 | 0.60 | 0.40 | 0.20 | 0.05 |
| I/A | 0.03 | 0.06 | 0.11 | 0.12 | 0.17 | 0.23 | 0.26 | 0.29 |
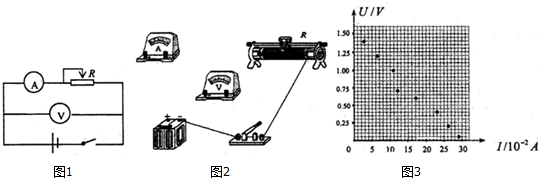
查看答案和解析>>
科目:高中物理 来源: 题型:多选题
| A. | 科学家研究“天宫一号”与“神州八号”的对接过程时可以将它们视为质点 | |
| B. | 因为参考系可以任意选择,所以选择不同参考系来观察同一物体的运动,其结果不会变化 | |
| C. | 因为矢量既有大小又有方向,所以有大小又有方向的物理量称为矢量 | |
| D. | 惯性是物体的本质属性,它反映了物体抵抗运动状态变化的本领,其大小由物体的质量来量度 |
查看答案和解析>>
科目:高中物理 来源: 题型:解答题

查看答案和解析>>
科目:高中物理 来源: 题型:解答题
查看答案和解析>>
科目:高中物理 来源: 题型:多选题
| A. | 同一个物体,运动时的惯性比静止时的大 | |
| B. | 公交车刹车时,人的身体会向前倾是因为有惯性 | |
| C. | 物体质量越大,惯性越大 | |
| D. | 物体受到的力越大,惯性越大 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com