
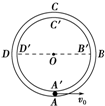
 如图所示,在竖直平面内固定有两个很靠近的同心圆形轨道,外圆ABCD光滑,内圆的上半部分B′C′D′粗糙,下半部分B′A′D′光滑.一质量为m=0.2kg的小球从外轨道的最低点A处以初速度v0向右运动,小球的直径略小于两圆的间距,小球运动的轨道半径R=0.2m,取g=10m/s2.
如图所示,在竖直平面内固定有两个很靠近的同心圆形轨道,外圆ABCD光滑,内圆的上半部分B′C′D′粗糙,下半部分B′A′D′光滑.一质量为m=0.2kg的小球从外轨道的最低点A处以初速度v0向右运动,小球的直径略小于两圆的间距,小球运动的轨道半径R=0.2m,取g=10m/s2.分析 (1)若要使小球始终紧贴着外圆做完整的圆周运动,在最高点时由重力提供向心力,由牛顿第二定律求最高点的临界速度,再由动能定理求初速度的最小值.
(2)由牛顿第二定律求出小球到达最高点的速度,再由动能定理求克服摩擦力做的功.
(3)经足够长的时间后,小球在下半圆轨道内做往复运动由动能定理求.
解答 解:(1)设此情形下小球到达外轨道的最高点的最小速度为vC,则由牛顿第二定律可得 mg=m$\frac{{v}^{2}}{R}$
由动能定理可知-2mgR=$\frac{1}{2}$mv2-$\frac{1}{2}$m${v}_{0}^{2}$
代入数据解得:v0=$\sqrt{10}$m/s.
(2)设此时小球到达最高点的速度为vC′,克服摩擦力做的功为W,则由牛顿第二定律可得 mg-FC=m$\frac{{v}_{C}^{′2}}{R}$
由动能定理可知-2mgR-W=$\frac{1}{2}$mvC′2-$\frac{1}{2}$m${v}_{0}^{2}$
代入数据解得:W=0.1 J
(3)经足够长的时间后,小球在下半圆轨道内做往复运动.设小球经过最低点的速度为vA,则由动能定理可知
mgR=$\frac{1}{2}$m${v}_{A}^{2}$
代入数据解得:vA=2 m/s
答:
(1)若要使小球始终紧贴着外圆做完整的圆周运动,初速度v0至少为$\sqrt{10}$m/s.
(2)小球在这段时间内克服摩擦力做的功是0.1J.
(3)若v0=3.1m/s,经过足够长的时间后,小球经过最低点A时速度vA为2m/s.
点评 本题综合考查了动能定理、牛顿第二定律和机械能守恒定律,关键是理清运动过程,抓住临界状态,运用合适的规律进行求解.


科目:高中物理 来源: 题型:填空题
查看答案和解析>>
科目:高中物理 来源: 题型:解答题
查看答案和解析>>
科目:高中物理 来源: 题型:选择题
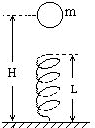 如图轻质弹簧长为L,竖直固定在地面上,质量为m的小球,由离地面高度为H处,由静止开始下落,正好落在弹簧上,使弹簧的最大压缩量为x,在下落过程中,小球受到的空气阻力恒为f,则弹簧在最短时具有的弹性势能为( )
如图轻质弹簧长为L,竖直固定在地面上,质量为m的小球,由离地面高度为H处,由静止开始下落,正好落在弹簧上,使弹簧的最大压缩量为x,在下落过程中,小球受到的空气阻力恒为f,则弹簧在最短时具有的弹性势能为( )| A. | (mg-f)(H-L+x) | B. | mg(H-L+x)-f(H-L) | C. | mgH-f(H-L) | D. | mg(L-x)+f(H-L+x) |
查看答案和解析>>
科目:高中物理 来源: 题型:选择题
| A. | 0 | B. | $\frac{1}{4}$mg | C. | $\frac{1}{9}$mg | D. | mg |
查看答案和解析>>
科目:高中物理 来源: 题型:解答题
查看答案和解析>>
科目:高中物理 来源: 题型:选择题
| A. | 中轨道卫星的线速度小于高轨道卫星的线速度 | |
| B. | 中轨道卫星的角速度小于同步卫星的角速度 | |
| C. | 若一周期为8h的中轨道卫星某时刻在同步卫星的正下方,则经过24h仍在该同步卫星的正下方 | |
| D. | 高轨道卫星的向心加速度小于同步卫星的向心加速度 |
查看答案和解析>>
科目:高中物理 来源: 题型:解答题
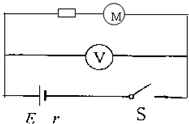 宜宾市小科学家协会的一位同学设计了一台玩具车,其内部结构的简化电路图如图所示.电源电动势为E,内阻r=1Ω,直流电动机M的线圈电阻R0=1Ω,与R=1Ω的保护电阻串联后接入电路中.电动机正常工作时,通过电动机的电流强度I=1A,电压表示数U=11V.求:
宜宾市小科学家协会的一位同学设计了一台玩具车,其内部结构的简化电路图如图所示.电源电动势为E,内阻r=1Ω,直流电动机M的线圈电阻R0=1Ω,与R=1Ω的保护电阻串联后接入电路中.电动机正常工作时,通过电动机的电流强度I=1A,电压表示数U=11V.求:查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com