
 质量为m的物块在平行于斜面的恒力F作用下,从倾角为θ的固定斜面底端A 由静止开始沿斜面上滑,经B点时速率为v,此时撤去F,物块滑回斜面底端时速率也为v,若A、B间距离为x,则(重力加速度为g)( )
质量为m的物块在平行于斜面的恒力F作用下,从倾角为θ的固定斜面底端A 由静止开始沿斜面上滑,经B点时速率为v,此时撤去F,物块滑回斜面底端时速率也为v,若A、B间距离为x,则(重力加速度为g)( )| A. | 整个过程中物块克服摩擦力做功为Fx-$\frac{1}{2}$mv2 | |
| B. | 滑块滑回底端时重力的瞬时功率为mgvcosθ | |
| C. | 下滑过程中物块重力做功为mgxsinθ[1+$\frac{{mv}^{2}}{{2Fx-mv}^{2}}$] | |
| D. | 从撤去F到物块滑回斜面底端,物体克服摩擦力做功为mgxsinθ |
分析 对整个运动过程应用动能定理求得克服摩擦力做的功,根据瞬时功率的定义求得滑块滑回底端时重力的瞬时功率;对AB运动过程和整个运动过程应用动能定理得到重力和摩擦力的合力做的功之比,然后根据AB运动过程克服重力做的功求得上滑过程克服重力做的功,即可得到下滑过程重力做的功;对撤去F到物块滑回斜面底端的运动过程应用动能定理求得克服摩擦力做的功.
解答 解:A、整个过程重力做功为零,故只有F和摩擦力做功,那么由动能定理可得:$Fx+{W}_{f}=\frac{1}{2}m{v}^{2}-0$,所以,整个过程中物块克服摩擦力做功为$-{W}_{f}=Fx-\frac{1}{2}m{v}^{2}$,故A正确;
B、滑块滑回底端时重力的瞬时功率为mgvsinθ,故B错误;
C、滑块从A到B,克服重力做功为mgxsinθ,由动能定理可知:克服重力和摩擦力做功为$Fx-\frac{1}{2}m{v}^{2}$;
从A到最高点,设克服重力做功为WG,由动能定理可知:克服重力和摩擦力做功为Fx;
物体在上滑过程重力、摩擦力不变,故有:$\frac{{W}_{G}}{mgxsinθ}=\frac{Fx}{Fx-\frac{1}{2}m{v}^{2}}$;
所以,${W}_{G}=mgxsinθ•\frac{Fx}{Fx-\frac{1}{2}m{v}^{2}}=mgxsinθ(1+\frac{m{v}^{2}}{2Fx-m{v}^{2}})$,
故下滑过程中物块重力做功为mgxsinθ[1+$\frac{{mv}^{2}}{{2Fx-mv}^{2}}$],故C正确;
D、从撤去F到物块滑回斜面底端,只有重力、摩擦力做功,故由动能定理可得:$mgxsinθ+{W}_{f2}=\frac{1}{2}m{v}^{2}-\frac{1}{2}m{v}^{2}=0$,
那么,从撤去F到物块滑回斜面底端,物体克服摩擦力做功为-Wf2=mgxsinθ,故D正确;
故选:ACD.
点评 经典力学问题一般先对物体进行受力分析,求得合外力及运动过程做功情况,然后根据牛顿定律、动能定理及几何关系求解.


 名校课堂系列答案
名校课堂系列答案科目:高中物理 来源: 题型:计算题
查看答案和解析>>
科目:高中物理 来源: 题型:选择题
 如图所示,光滑板球面上有A、B两个用轻绳相连的小球处于静止状态,两小球质量分别为mA、mB,对地面的压力分别为NA、NB,过两小球的半径与竖直方向的夹角分别为θ1、θ2.下列说法正确的是( )
如图所示,光滑板球面上有A、B两个用轻绳相连的小球处于静止状态,两小球质量分别为mA、mB,对地面的压力分别为NA、NB,过两小球的半径与竖直方向的夹角分别为θ1、θ2.下列说法正确的是( )| A. | $\frac{{m}_{A}}{{m}_{B}}$=$\frac{sin{θ}_{1}}{sin{θ}_{2}}$ | B. | $\frac{{m}_{A}}{{m}_{B}}$=$\frac{tan{θ}_{1}}{tan{θ}_{2}}$ | ||
| C. | $\frac{{N}_{A}}{{N}_{B}}$=$\frac{sin{θ}_{2}}{sin{θ}_{1}}$ | D. | $\frac{{N}_{A}}{{N}_{B}}$=$\frac{tan{θ}_{2}}{tan{θ}_{1}}$ |
查看答案和解析>>
科目:高中物理 来源: 题型:选择题
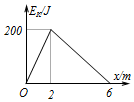 物块在水平桌面上受到水平恒定拉力作用下由静止开始加速运动,经过一段时间后撤去拉力,物块又滑行一段距离停下来.如果以物块的初始位置为坐标原点,沿运动方向建立x轴,则物块的动能Ek随位置坐标x的变化图象如图所示.重力加速度为已知量,根据图象可以求出下面哪些量( )
物块在水平桌面上受到水平恒定拉力作用下由静止开始加速运动,经过一段时间后撤去拉力,物块又滑行一段距离停下来.如果以物块的初始位置为坐标原点,沿运动方向建立x轴,则物块的动能Ek随位置坐标x的变化图象如图所示.重力加速度为已知量,根据图象可以求出下面哪些量( )| A. | 物块的质量 | |
| B. | 物块与桌面之间的动摩擦因数 | |
| C. | 水平拉力大小 | |
| D. | 物块在前0~2m和后2m~4m内的加速度 |
查看答案和解析>>
科目:高中物理 来源: 题型:计算题
查看答案和解析>>
科目:高中物理 来源: 题型:计算题
 质量为50kg的空箱子放在光滑水平面上,箱子中有一同样质量的铁块,铁块与箱子的左壁相距10m,它一旦与左壁相碰将会瞬间粘在一起,然后不再分开,铁块与箱底的摩擦不计.用水平向右的推力10N作用于箱子,12s后立即去掉推力.求撤去推力瞬间箱子与铁块的共同速度.
质量为50kg的空箱子放在光滑水平面上,箱子中有一同样质量的铁块,铁块与箱子的左壁相距10m,它一旦与左壁相碰将会瞬间粘在一起,然后不再分开,铁块与箱底的摩擦不计.用水平向右的推力10N作用于箱子,12s后立即去掉推力.求撤去推力瞬间箱子与铁块的共同速度.查看答案和解析>>
科目:高中物理 来源: 题型:实验题
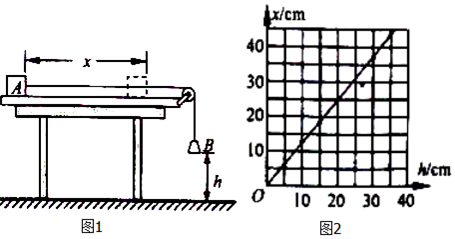
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com