
 如图所示,在粗糙水平台阶上静止放置一质量m=0.5kg的小物块,它与水平台阶表面的动摩擦因数μ=0.5,且与台阶边缘O点的距离s=5m.在台阶右侧固定了一个$\frac{1}{4}$圆弧挡板,圆弧半径R=1m,圆弧的圆心也在O点.今以O点为原点建立平面直角坐标系.现用F=5N的水平恒力拉动小物块,一段时间后撤去拉力,小物块最终水平抛出并击中挡板.(g取10m/s2)
如图所示,在粗糙水平台阶上静止放置一质量m=0.5kg的小物块,它与水平台阶表面的动摩擦因数μ=0.5,且与台阶边缘O点的距离s=5m.在台阶右侧固定了一个$\frac{1}{4}$圆弧挡板,圆弧半径R=1m,圆弧的圆心也在O点.今以O点为原点建立平面直角坐标系.现用F=5N的水平恒力拉动小物块,一段时间后撤去拉力,小物块最终水平抛出并击中挡板.(g取10m/s2)分析 (1)根据平抛知识求小物块离开O点时的速度大小;
(2)小物块能击中挡板,则小物块必须能够到达O点,据动能定理求得力F作用的位移,再根据牛顿运动定律和运动学规律求得力F的作用时间;
(3)根据能击中挡板的条件求出小物块动能的表达式,再根据数学分析求动能的最小值.
解答 解:(1)小物块从O到P,做平抛运动
水平方向:Rcos37°=v0t
竖直方向:$Rsin37°=\frac{1}{2}g{t}^{2}$
可得:${v}_{0}=\frac{Rcos37°}{t}=\frac{Rcos37°}{\sqrt{\frac{2Rsin37°}{g}}}$=$\frac{4}{3}\sqrt{3}m/s$
(2)为使小物块击中档板,小物块必须能运动到O点,
由动能定理得:Fx-μmgS=△Ek=0
解得:$x=\frac{μmg}{F}S=\frac{0.5×0.5×10}{5}×5m$=2.5m
由牛顿第二定律得:F-μmg=ma
解得:$a=\frac{F}{m}-μg=\frac{5}{0.5}-0.5×10m/{s}^{2}=5m/{s}^{2}$
由运动学公式得:$x=\frac{1}{2}a{t}^{2}$
解得:t=1s
(3)设小物块击中挡板的任意点坐标为(x,y),则
x=v0t
$y=\frac{1}{2}g{t}^{2}$
由机械能守恒得:${E}_{k}=\frac{1}{2}m{v}_{0}^{2}+mgy$
又x2+y2=R
化简整理得:${E}_{k}=\frac{mg{R}^{2}}{4y}+\frac{3mgy}{4}$
由数学知识可得${E}_{kmin}=\frac{5\sqrt{3}}{2}J$
答:(1)若小物块击中档板上的P点(OP与水平方向夹角为37°,已知sin37°=0.6,cos37°=0.8)则其离开O点时的速度大小为$\frac{4}{3}\sqrt{3}m/s$;
(2)为使小物块击中档板,拉力F作用的最短时间为1s;
(3)改变拉力F的作用时间,使小物块击中挡板的不同位置.击中挡板时小物块动能的最小值为$\frac{5\sqrt{3}}{2}J$.
点评 解决本题的关键是掌握平抛运动知识及牛顿运动定律和动能定理的应用,本题综合性较高,需要掌握的知识点较多,题目较难.


 愉快的寒假南京出版社系列答案
愉快的寒假南京出版社系列答案科目:高中物理 来源: 题型:填空题
查看答案和解析>>
科目:高中物理 来源: 题型:填空题
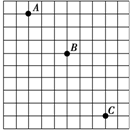 如图所示为一小球做平抛运动的闪光照片的一部分,图中背景方格的边长均为5cm,如果g取10m/s2,那么:
如图所示为一小球做平抛运动的闪光照片的一部分,图中背景方格的边长均为5cm,如果g取10m/s2,那么:查看答案和解析>>
科目:高中物理 来源: 题型:选择题
| A. | 月球车处于失重状态 | |
| B. | 月球车处于超重状态 | |
| C. | 月球车不受月球的作用力 | |
| D. | 着陆器为月球车提供绕月运动的向心力 |
查看答案和解析>>
科目:高中物理 来源: 题型:选择题
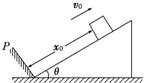 如图所示,斜面的倾角为θ,质量为m的滑块距挡板P的距离为x0,滑块以初速度v0沿斜面上滑,滑块与斜面间的动摩擦因数为μ,滑块所受摩擦力小于重力沿斜面向下的分力.若滑块每次与挡板相碰均无机械能损失,滑块经过的总路程是( )
如图所示,斜面的倾角为θ,质量为m的滑块距挡板P的距离为x0,滑块以初速度v0沿斜面上滑,滑块与斜面间的动摩擦因数为μ,滑块所受摩擦力小于重力沿斜面向下的分力.若滑块每次与挡板相碰均无机械能损失,滑块经过的总路程是( )| A. | $\frac{1}{μ}$($\frac{{{v}_{0}}^{2}}{2gcosθ}$+x0tanθ) | B. | $\frac{1}{μ}$($\frac{{{v}_{0}}^{2}}{2gsinθ}$+x0tanθ) | ||
| C. | $\frac{2}{μ}$($\frac{{{v}_{0}}^{2}}{2gcosθ}$+x0tanθ) | D. | $\frac{1}{μ}$($\frac{{{v}_{0}}^{2}}{2gcosθ}$+x0cotθ) |
查看答案和解析>>
科目:高中物理 来源: 题型:填空题
查看答案和解析>>
科目:高中物理 来源: 题型:解答题
 电阻可忽略的光滑平行金属导轨长S=1.3m,两导轨间距L=0.75m,导轨倾角为30°,导轨上端ab接一阻值R=1.5Ω的电阻,磁感应强度B=0.8T的匀强磁场垂直轨道平面向上.阻值r=0.5Ω,质量m=0.2kg的金属棒与轨道垂直且接触良好,从轨道上端ab处由静止开始下滑至底端,在此过程中金属棒产生的焦耳热Q=0.1J.(取g=10m/s2)求:
电阻可忽略的光滑平行金属导轨长S=1.3m,两导轨间距L=0.75m,导轨倾角为30°,导轨上端ab接一阻值R=1.5Ω的电阻,磁感应强度B=0.8T的匀强磁场垂直轨道平面向上.阻值r=0.5Ω,质量m=0.2kg的金属棒与轨道垂直且接触良好,从轨道上端ab处由静止开始下滑至底端,在此过程中金属棒产生的焦耳热Q=0.1J.(取g=10m/s2)求:查看答案和解析>>
科目:高中物理 来源: 题型:选择题
| A. | 36次 | B. | 12次 | C. | 6次 | D. | 4/3次 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com