
 完全相同的十三个扁长木块紧挨着放在水平地面上,如图所示,每个木块的质量m=0.40kg,长度L=0.5m.它们与地面间的动摩擦因数为μ1=0.10,原来所有木块处于静止状态.左方第一个木块的左端上方放一质量为M=1.0kg的小铅块,它与木块间的动摩擦因数为μ2=0.20.物体所受最大静摩擦力与滑动摩擦力相等,现突然给铅块一向右的初速度v0=5m/s,使其开始在木块上滑行.(重力加速度g=10m/s2,设铅块的长度与木块长度L相比可以忽略.)
完全相同的十三个扁长木块紧挨着放在水平地面上,如图所示,每个木块的质量m=0.40kg,长度L=0.5m.它们与地面间的动摩擦因数为μ1=0.10,原来所有木块处于静止状态.左方第一个木块的左端上方放一质量为M=1.0kg的小铅块,它与木块间的动摩擦因数为μ2=0.20.物体所受最大静摩擦力与滑动摩擦力相等,现突然给铅块一向右的初速度v0=5m/s,使其开始在木块上滑行.(重力加速度g=10m/s2,设铅块的长度与木块长度L相比可以忽略.)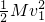 -
-
 m/s
m/s =-μ2g=-2m/s2
=-μ2g=-2m/s2 =0.25m/s2
=0.25m/s2 =2(a0-a1)L
=2(a0-a1)L >0
>0 =1.5m/s2
=1.5m/s2 =0.107m<L
=0.107m<L

科目:高中物理 来源: 题型:
 完全相同的十三个扁长木块紧挨着放在水平地面上,如图所示,每个木块的质量m=0.40kg,长度L=0.5m.它们与地面间的动摩擦因数为μ1=0.10,原来所有木块处于静止状态.左方第一个木块的左端上方放一质量为M=1.0kg的小铅块,它与木块间的动摩擦因数为μ2=0.20.物体所受最大静摩擦力与滑动摩擦力相等,现突然给铅块一向右的初速度v0=5m/s,使其开始在木块上滑行.(重力加速度g=10m/s2,设铅块的长度与木块长度L相比可以忽略.)
完全相同的十三个扁长木块紧挨着放在水平地面上,如图所示,每个木块的质量m=0.40kg,长度L=0.5m.它们与地面间的动摩擦因数为μ1=0.10,原来所有木块处于静止状态.左方第一个木块的左端上方放一质量为M=1.0kg的小铅块,它与木块间的动摩擦因数为μ2=0.20.物体所受最大静摩擦力与滑动摩擦力相等,现突然给铅块一向右的初速度v0=5m/s,使其开始在木块上滑行.(重力加速度g=10m/s2,设铅块的长度与木块长度L相比可以忽略.)查看答案和解析>>
科目:高中物理 来源:2009年江苏省宿迁市高考物理模拟试卷(四)(解析版) 题型:解答题

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com