练习册

  • 练习册
  • 试题
    精英家教网 > 高中物理 > 题目详情
    12．如图所示，物体A、B叠放在一起，A用绳系在固定的墙上，用力F将B拉着右移，用T、fAB、fBA分别表示绳中拉力、A对B的摩擦力和B对A的摩擦力，则下面叙述中正确的是（　　）
    A．F做正功，fAB做负功，fBA做正功，T不做功
    B．F做正功，fAB做负功，fBA和T不做功
    C．F、fBA做正功，fAB、T不做功
    D．F做正功，其他力都不做功

    分析 B的受力情况：B向右直线运动，水平方向受到拉力和摩擦力，拉力和摩擦力不一定是一对平衡力；物体间力的作用是相互的，A对B的摩擦和B对A的摩擦是相互作用力，大小相等；功是力与力的方向位移的乘积，当两者夹角小于90°时此力做正功，当两者夹角大于90°时此力做负功

    解答 解：
    由题意可知，A不动B向右运动，但均受到滑动摩擦力，由于B相对A向右运动，故其受到的摩擦力fAB向左，与位移方向相反，做负功；拉力F与位移同向，做正功；
    由于A没有位移，所以绳的拉力T和fBA不做功．故B正确；ACD错误；
    故选：B

    点评 （1）平衡力和相互作用力很相似，容易混淆，注意区分：相同点：大小相等、方向相反、在同一条直线上．不同点：平衡力作用在同一物体上，相互作用力作用在两个物体上．
    （2）静止不一定受到静摩擦力，滑动不一定受到滑动摩擦力；
    （3）功的正负是由力与位移方向的夹角决定，当夹角小于90°力做正功；当夹角大于90°力做负功

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中物理 来源： 题型：填空题

    2．在对称负载的三相交流电路中，中线上的电流为0．

    查看答案和解析>>

    科目：高中物理 来源： 题型：多选题

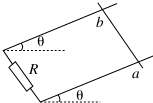    3．处于竖直向上的匀强磁场中的两根电阻不计的平行金属导轨，下端连一电阻R，导轨与水平面之间的夹角为θ．一电阻可忽略的金属棒ab，开始固定在两导轨上某位置，棒与导轨垂直，如图所示．现释放金属棒让其由静止开始沿轨道平面下滑．对导轨光滑和粗糙两种情况进行比较，当两次下滑的位移相同时，则有（　　）
    A．重力势能的减小量相同B．机械能的变化量相同
    C．磁通量的变化量相同D．安培力做功相同

    查看答案和解析>>

    科目：高中物理 来源： 题型：选择题

    20．下列叙述中符合物理学史实的有（　　）
    A．德布罗意提出了实物粒子也具有波动性
    B．玻尔通过α粒子散射实验，提出了原子的核式结构学说
    C．汤姆生发现了质子
    D．居里夫妇首先发现了天然放射现象

    查看答案和解析>>

    科目：高中物理 来源： 题型：填空题

    7．如图所示，框架面积为S，框架平面与磁感应强度为B的匀强磁场方向垂直，则穿过平面的磁通量为BS．若使框架绕OO′转过60°角，则穿过框架平面的磁通量为$\frac{1}{2}$BS．

    查看答案和解析>>

    科目：高中物理 来源： 题型：填空题

    17．一列简谐横波在x轴上传播，t=0时刻的波形如图（a）所示，x=2m的质点P的振动图象如图（b）所示，那么，由此可以判断：

    （1）波的传播方向是沿x轴负方向；
    （2）在0到5s时间内质点P通过的路程是25cm．

    查看答案和解析>>

    科目：高中物理 来源： 题型：选择题

    4．物体在万有引力场中具有的势能叫做引力势能，取两物体相距无穷远时的引力势能为零，一个质量为m0的质点距质量为M0的引力源中心为r0时，其引力势能EP=-$\frac{G{M}_{0}{m}_{0}}{{r}_{0}}$（式中G为引力常数）．一颗质量为m的人造地球卫星以圆形轨道环绕地球飞行，已知地球的质量为M，由于受高空稀薄空气的阻力作用，卫星的圆轨道半径从r1逐渐减小到r2，若在这个过程中空气阻力做功为Wt，则在下面给出的Wt的四个表达式中正确的是（　　）
    A．Wt=-$\frac{GMm}{3}$（$\frac{1}{{r}_{2}}$-$\frac{1}{{r}_{1}}$）B．Wt=-GMm（$\frac{1}{{r}_{1}}$-$\frac{1}{{r}_{2}}$）C．Wt=-$\frac{GMm}{2}$（$\frac{1}{{r}_{2}}$-$\frac{1}{{r}_{1}}$）D．Wt=-$\frac{GMm}{3}$（$\frac{1}{{r}_{1}}$-$\frac{1}{{r}_{2}}$）

    查看答案和解析>>

    科目：高中物理 来源： 题型：多选题

    1．高铁每节车厢都有两间洗手间，只有当两间洗手间的门都关上时（每扇门的插销都相当于一个开关），车厢中指示牌内的指示灯才会发光提示旅客“洗手间有人”．下列所示电路图不能实现上述目标的是（　　）
    A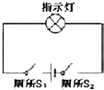．B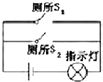．C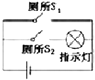．D．

    查看答案和解析>>

    科目：高中物理 来源： 题型：选择题

    14．在倾角为α的斜面上，一木块向上滑动，经t秒时间滑行L距离而停止，则木块与斜面间的动摩擦因数和木块再下滑至斜面底端所用的时间分别为（　　）
    A．$\frac{2L}{g{t}^{2}cosα}$-tanα，t$\sqrt{\frac{L}{g{t}^{2}sinα-L}}$B．$\frac{Lcosα}{g{t}^{2}}$-tanα，t$\sqrt{\frac{gL}{{t}^{2}sinα-L}}$
    C．$\frac{Lsinα}{{t}^{2}}$-cosα，t$\sqrt{\frac{gL}{{t}^{2}cosα-L}}$D．$\frac{Ltanα}{g{t}^{2}}$-cosα，t$\sqrt{\frac{2gL}{g{t}^{2}-L}}$

    查看答案和解析>>

    同步练习册答案