
 质量m=0.2kg的物体在光滑的水平面上运动,运动的起点为一直角坐标系的坐标原点,其分速度vx和vy随时间变化的图线如图所示,求:
质量m=0.2kg的物体在光滑的水平面上运动,运动的起点为一直角坐标系的坐标原点,其分速度vx和vy随时间变化的图线如图所示,求:分析 (1)由图读出t=0s时x轴和y轴方向的分速度,合成求出物体的初速度,根据速度的合成法则,即可求解第4s末的速度;
(2)物体在x轴方向做匀速直线运动,y轴方向做匀加速运动,分别求出两个方向的分位移,再合成求解物体的位移;
(3)由两方向的位移与时间表达式,从而将时间消去,即可求解.
解答 解:(1)由图读出t=0s时x轴和y轴方向的分速度分别为:0与4m/s,
根据速度的合成可知,物体的初速度为4m/s;
t=4s时,vx=4m/s,vy=4m/s,则v=$\sqrt{{v}_{x}^{2}+{v}_{y}^{2}}$=$\sqrt{{4}^{2}+{4}^{2}}$=4$\sqrt{2}$ m/s
tanθ=$\frac{{v}_{y}}{{v}_{x}}$=$\frac{4}{4}$=1,即速度方向与x轴正方向成45°偏正y方向.
(3)t=4s时,y=vyt=16m,
x=$\frac{1}{2}$at2=$\frac{1}{2}$×1×42=8m
故S=$\sqrt{{x}^{2}+{y}^{2}}$=$\sqrt{{8}^{2}+1{6}^{2}}$=8$\sqrt{5}$m,
tanα=$\frac{x}{y}$=$\frac{8}{16}$=$\frac{1}{2}$,
α=arctan$\frac{1}{2}$,
即位移方向与速度方向与x轴正方向成arctan$\frac{1}{2}$ 偏正y方向.
(3)根据x的方向位移与时间关系,x=$\frac{1}{2}$at2=$\frac{1}{2}{t}^{2}$
而y方向的位移与时间的关系,y=vyt=4t;
解得:y=4$\sqrt{2x}$;
答:(1)物体的初速度4m/s;4s末物体的速度4$\sqrt{2}$ m/s,与x轴正方向成45°偏正y方向;
(2)位移8$\sqrt{5}$ m,与x轴正方向成arctan$\frac{1}{2}$偏正y方向.
(3)物体运动的轨迹方程y=4$\sqrt{2x}$.
点评 本题是运动的合成问题,包括加速度、速度、位移的合成,都按平行四边形定则进行合成.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中物理 来源: 题型:解答题
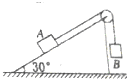 在倾角为30°的斜面上放着一个质量M=2 kg的物体A,由轻绳与质量为m物体B相连,如图所示.已知A与斜面的动摩擦因素μ=0.1.(g取10N/kg)求:
在倾角为30°的斜面上放着一个质量M=2 kg的物体A,由轻绳与质量为m物体B相连,如图所示.已知A与斜面的动摩擦因素μ=0.1.(g取10N/kg)求:查看答案和解析>>
科目:高中物理 来源: 题型:解答题
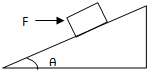 如图所示,质量为m的物体,不施加外力时,恰好能在斜面匀速下滑,已知斜面和物体之间的动摩擦因素为μ,那么要将物体匀速推上斜面,必须施加的水平推力为多大?
如图所示,质量为m的物体,不施加外力时,恰好能在斜面匀速下滑,已知斜面和物体之间的动摩擦因素为μ,那么要将物体匀速推上斜面,必须施加的水平推力为多大?查看答案和解析>>
科目:高中物理 来源: 题型:解答题
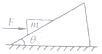 如图所示,楔形木块质量为m,放在倾角θ的斜面上,已知木块与斜面间的动摩擦因数为μ(μ<tanθ),今用水平力F推木块,木块恰好沿斜面向上作匀速运动(斜面保持静止).试求推力的大小.
如图所示,楔形木块质量为m,放在倾角θ的斜面上,已知木块与斜面间的动摩擦因数为μ(μ<tanθ),今用水平力F推木块,木块恰好沿斜面向上作匀速运动(斜面保持静止).试求推力的大小.查看答案和解析>>
科目:高中物理 来源: 题型:解答题
 质量为2Kg的物体,从竖直平面内高h=1.0m的光滑弧形轨道A点以v0=4.0m/s的初速度沿轨道滑下,并进入水平BC轨道滑行6.0m后停下来,如图所示.求:
质量为2Kg的物体,从竖直平面内高h=1.0m的光滑弧形轨道A点以v0=4.0m/s的初速度沿轨道滑下,并进入水平BC轨道滑行6.0m后停下来,如图所示.求:查看答案和解析>>
科目:高中物理 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com