
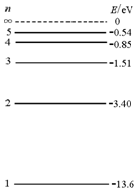
| A�� | һ������ n=2 �ܼ�����ԭ�ӣ���������һ������Ϊ 4eV �Ĺ��� | |
| B�� | ������ԭ�ӴӸ��ܼ��� n=3 �ܼ�ԾǨʱ�������Ĺ��Dz��ɼ��� | |
| C�� | �������� n=4 �ܼ�����ԭ�ӣ�ԾǨ����̬�Ĺ����п����ͷų� 6 ��Ƶ�ʵĹ��� | |
| D�� | ��ԭ�ӴӸ��ܼ�����ܼ�ԾǨ�Ĺ������ͷŵĹ��ӵ��������ܴ��� 13.6eV |
���� ��ԭ�����չ����������������ڵ����㣬�ᷢ�����룮������ѧ��Ϲ�ʽ�ó���ԭ��ԾǨʱ���ܷ�����ͬƵ�ʹ��ӵ�������ץס����Ĺ��������������ܼ�����ܼ�����������Ĺ��Ƿ��Dz��ɼ��⣮
��� �⣺A��һ������ n=2 �ܼ�����ԭ�ӣ���������Ϊ4eV�Ĺ��ӻᷢ�����룬��A��ȷ��
B��������ԭ�ӴӸ��ܼ��� n=3 �ܼ�ԾǨʱ����������ֹ��������ֱ�Ϊ��12.09eV��1.89eV��10.2eV������1.62��3.11eV��Χ֮�ڣ������Ĺⶼ�Dz��ɼ��⣬��B��ȷ��
C������${C}_{4}^{2}$=6֪���������� n=4 �ܼ�����ԭ�ӣ�ԾǨ����̬�Ĺ����п����ͷų� 6 ��Ƶ�ʵĹ��ӣ���C��ȷ��
D�����ܼ�ͼ��֪����ԭ�ӴӸ��ܼ�����ܼ�ԾǨ�Ĺ������ͷŵĹ��ӵ����������ܴ���13.6eV����D����
��ѡ��ABC��
���� �������Ĺؼ�֪��ԭ�ӴӸ��ܼ�����ܼ�ԾǨ���Թ��ӵ���ʽ�������������������Ĺ�������ǡ���ڷ���ԾǨʱ�����ܼ���������


 �Ķ��쳵ϵ�д�
�Ķ��쳵ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ���������� ��Դ�� ���ͣ������
 ��ͼ��ʾ������ƽ���㹻���Ĺ⻬����������ֱ���ã����L=1m��������Բ��ƣ������϶˽�һ��ֵΪR=0.5���ĵ��裬���촦�ڴ�ֱ�ڹ��ƽ�����ǿ�ų��У������ab������m=0.1kg������r=0.5�����ɾ�ֹ��ʼ�ڵ�������Ħ�����»�������������R�ĵ������������մﵽ���ֵI=1A�������˶�������ab��������ֱ���ҽӴ����ã�g=10m/s2����
��ͼ��ʾ������ƽ���㹻���Ĺ⻬����������ֱ���ã����L=1m��������Բ��ƣ������϶˽�һ��ֵΪR=0.5���ĵ��裬���촦�ڴ�ֱ�ڹ��ƽ�����ǿ�ų��У������ab������m=0.1kg������r=0.5�����ɾ�ֹ��ʼ�ڵ�������Ħ�����»�������������R�ĵ������������մﵽ���ֵI=1A�������˶�������ab��������ֱ���ҽӴ����ã�g=10m/s2�����鿴�𰸺ͽ���>>
��Ŀ���������� ��Դ�� ���ͣ�ʵ����
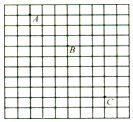 ��ͼ��һλͬѧ��ʵ�����������С����ƽ���˶���Ƶ����Ƭ��һ���֣���������ʱ�������û�а��ϱ�������壬ͼ�з����Ǻ����ó�������Ƭ�ϻ��ģ�ͼ�и��ӵ���ֱ����ʵ�����ش��ߵķ���ÿС��ı߳���Ϊ5cm����ȡ�������ٶ�gȡ10m/s2������
��ͼ��һλͬѧ��ʵ�����������С����ƽ���˶���Ƶ����Ƭ��һ���֣���������ʱ�������û�а��ϱ�������壬ͼ�з����Ǻ����ó�������Ƭ�ϻ��ģ�ͼ�и��ӵ���ֱ����ʵ�����ش��ߵķ���ÿС��ı߳���Ϊ5cm����ȡ�������ٶ�gȡ10m/s2�������鿴�𰸺ͽ���>>
��Ŀ���������� ��Դ�� ���ͣ�ѡ����
| A�� | ������ƽ | B�� | ���� | C�� | ���ɲ����� | D�� | ˮ����ѹ�� |
�鿴�𰸺ͽ���>>
��Ŀ���������� ��Դ�� ���ͣ�ѡ����
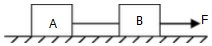
| A�� | F2=F1 | B�� | F1��F2 | C�� | F2��F1 | D�� | F1=��F2 |
�鿴�𰸺ͽ���>>
��Ŀ���������� ��Դ�� ���ͣ���ѡ��
 ��֪�ɼ�����ӵ��ܳ���1.64eV-3.19eV֮�䣬��ԭ�ӵ��ܼ�ͼ��ͼ��ʾ�����д�����ԭ�Ӵ���������n=5���ܼ�״̬������˵����ȷ���ǣ�������
��֪�ɼ�����ӵ��ܳ���1.64eV-3.19eV֮�䣬��ԭ�ӵ��ܼ�ͼ��ͼ��ʾ�����д�����ԭ�Ӵ���������n=5���ܼ�״̬������˵����ȷ���ǣ�������| A�� | ��ԭ���ɸ��ܼ�����ܼ�ԾǨʱ��������ӵĶ��ܡ������ܾ���С | |
| B�� | ��ԭ���ɸ��ܼ�����ܼ�ԾǨʱ��������ӵĶ�������������ܼ�С | |
| C�� | ��Щ��ԭ�ӿ��ܷ���4��Ƶ�ʵĹ��ӣ��������ڿɼ�����ӵ���1�� | |
| D�� | ��Щ��ԭ�ӿ��ܷ���10��Ƶ�ʵĹ��ӣ��������ڿɼ�����ӵ���3�� |
�鿴�𰸺ͽ���>>
��Ŀ���������� ��Դ�� ���ͣ�ѡ����

| A�� | A���뱾����ǿ | B�� | BΪ��X���߲��������Ĺ����� | ||
| C�� | һ��ֽƬ�Ϳ��Խ�C��ס | D�� | AΪ���ٵ�����ɵĵ����� |
�鿴�𰸺ͽ���>>
��Ŀ���������� ��Դ�� ���ͣ������
 �������س������ػ���ߴ����ͽ������ϣ�����߶�Ϊh��¥�����ͽ������ϣ��������ϵ���h�ߴ��ٶ�ǡ��Ϊ0���������ϵ�v-tͼ������ػ���P-tͼ����ͼ��ʾ������һ��Ħ����g=10m/s2����
�������س������ػ���ߴ����ͽ������ϣ�����߶�Ϊh��¥�����ͽ������ϣ��������ϵ���h�ߴ��ٶ�ǡ��Ϊ0���������ϵ�v-tͼ������ػ���P-tͼ����ͼ��ʾ������һ��Ħ����g=10m/s2�����鿴�𰸺ͽ���>>
��Ŀ���������� ��Դ�� ���ͣ�ѡ����
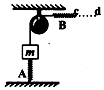 ��ͼ��ʾ������ϵ��Ϊk1�����ʵ���Aһ�˹̶��ڵ����ϲ���ֱ���ã�����Ϊm�����ѹ�ڵ���A�ϣ���һϸ����������֣�һ����m��������һ���뾢��ϵ��Ϊk2�����ʵ���B���������������ŵ���B���Ҷ�ʹ��λ��c��ʱ������Bǡ�ó�ˮƽ��û���α䣮������B���Ҷ�ˮƽ����d��ʱ������Aǡ��û���α䣬��֪k1��k2����c��d֮��ľ���Ϊ��������
��ͼ��ʾ������ϵ��Ϊk1�����ʵ���Aһ�˹̶��ڵ����ϲ���ֱ���ã�����Ϊm�����ѹ�ڵ���A�ϣ���һϸ����������֣�һ����m��������һ���뾢��ϵ��Ϊk2�����ʵ���B���������������ŵ���B���Ҷ�ʹ��λ��c��ʱ������Bǡ�ó�ˮƽ��û���α䣮������B���Ҷ�ˮƽ����d��ʱ������Aǡ��û���α䣬��֪k1��k2����c��d֮��ľ���Ϊ��������| A�� | $\frac{{k}_{1}+{k}_{2}}{{k}_{1}{k}_{2}}$mg | B�� | $\frac{{k}_{1}-{k}_{2}}{{k}_{1}{k}_{2}}$mg | C�� | $\frac{mg}{{k}_{1}+{k}_{2}}$ | D�� | $\frac{mg}{{k}_{1}-{k}_{2}}$ |
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com