
 ��ͼ��ʾ���뾶R=0.4m�Ĺ⻬��Բ�����������ֱƽ���ڣ���Բ����ֲڵ�ˮƽ����������Բ���Ķ˵�A��һ����m=0.1kg��С���Գ��ٶ�v0=7.0m/s��ˮƽ���������������ٶ�a=3.0m/s2���ȼ���ֱ���˶����˶�L=4m������ֱ��Բ�������С������C�㣮���������ٶ�g=10m/s2����
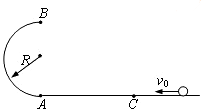
��ͼ��ʾ���뾶R=0.4m�Ĺ⻬��Բ�����������ֱƽ���ڣ���Բ����ֲڵ�ˮƽ����������Բ���Ķ˵�A��һ����m=0.1kg��С���Գ��ٶ�v0=7.0m/s��ˮƽ���������������ٶ�a=3.0m/s2���ȼ���ֱ���˶����˶�L=4m������ֱ��Բ�������С������C�㣮���������ٶ�g=10m/s2�������� ��1�������ȱ���ֱ���˶����ٶ�λ�ƹ�ʽ��������˶���A����ٶȴ�С��
��2�����ݶ��ܶ������С��B����ٶȣ����ţ�ٵڶ����������B������С��ĵ�����
��3�����ݸ߶����ƽ���˶���ʱ�䣬���B����ٶ����A��C�����ľ���d��
��� �⣺��1��С���������ȼ���ֱ���˶��������ٶ�λ�ƹ�ʽ�У�${{v}_{A}}^{2}-{{v}_{0}}^{2}=2aL$��
���${v}_{A}=\sqrt{{{v}_{0}}^{2}+2aL}=\sqrt{49-2��3��4}$m/s=5m/s��
��2�����ݶ��ܶ����ã�$-2mgR=\frac{1}{2}m{{v}_{B}}^{2}-\frac{1}{2}m{{v}_{A}}^{2}$��
�������ݽ��vB=3m/s��
����ţ�ٵڶ����ɵã�mg+FB=m$\frac{{v}_{B}^{2}}{R}$��
�������ݽ��FB=1.25N��
����ţ�ٵ�������֪��С��B��ʱ�Թ����ѹ����СΪ1.25N��
��3������2R=$\frac{1}{2}g{t}^{2}$�ã�ƽ���˶���ʱ��t=$\sqrt{\frac{4R}{g}}=\sqrt{\frac{4��0.4}{10}}s=0.4s$��
��A��C�����ľ���d=vBt=3��0.4m=1.2m��
�𣺣�1�������˶���A��ʱ���ٶȴ�СΪ5m/s��
��2��С��B��ʱ�Թ����ѹ����СΪ1.25N��
��3��A��C�����ľ���Ϊ1.2m��
���� ���⿼����ƽ���˶���Բ���˶��Ͷ��ܶ�����ţ�ٶ��ɵ��ۺ����ã�֪��Բ���˶�����������Դ�Լ�ƽ���˶���ˮƽ�������ֱ�����ϵ��˶������ǽ������Ĺؼ���



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ���������� ��Դ�� ���ͣ������
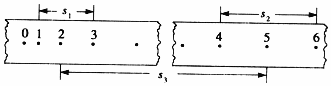 �ڡ����õ����ʱ���ⶨС�����ȱ����˶��ļ��ٶȡ���ʵ���У����������в���Ҫ���Ǣ٢ܢࣨ�ô��ű�ʾ����
�ڡ����õ����ʱ���ⶨС�����ȱ����˶��ļ��ٶȡ���ʵ���У����������в���Ҫ���Ǣ٢ܢࣨ�ô��ű�ʾ�����鿴�𰸺ͽ���>>
��Ŀ���������� ��Դ�� ���ͣ���ѡ��
| A�� | ���ҹ����ص����嶼����ͬ�Ľ��ٶ� | |
| B�� | ���е��������ٶȶ���� | |
| C�� | λ�ڳ����������������ٶȱ�λ�����������Ĵ� | |
| D�� | ������������������ļ��ٶȵķ���ָ����� |
�鿴�𰸺ͽ���>>
��Ŀ���������� ��Դ�� ���ͣ���ѡ��
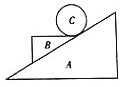 ��ͼ��ʾ���⻬ˮƽ��������һ��б��Ϊ30���б����A��������ľ��B��ֹ��A�ϣ�ľ��B�ϱ���ˮƽ�����⻬С��C������ľ��B�ϣ�A��B��C��������Ϊ1kg��б����A��ˮƽ����F��������3m/s2�ļ��ٶ���������˶����˶�������A��B��Cʼ����Ծ�ֹ��gȡ10m/s2��������
��ͼ��ʾ���⻬ˮƽ��������һ��б��Ϊ30���б����A��������ľ��B��ֹ��A�ϣ�ľ��B�ϱ���ˮƽ�����⻬С��C������ľ��B�ϣ�A��B��C��������Ϊ1kg��б����A��ˮƽ����F��������3m/s2�ļ��ٶ���������˶����˶�������A��B��Cʼ����Ծ�ֹ��gȡ10m/s2��������| A�� | С��C�ܵ����������� | B�� | С��C�ܵ����������� | ||
| C�� | С��B�ܵ����������� | D�� | ��F��СΪ9N |
�鿴�𰸺ͽ���>>
��Ŀ���������� ��Դ�� ���ͣ�ѡ����
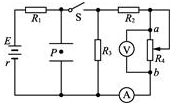 ��ͼ��ʾ������S�պϺ����ʵ���ƽ�н�������P��λ�ô��ھ�ֹ״̬��ͼ�е������Ϊ��������������
��ͼ��ʾ������S�պϺ����ʵ���ƽ�н�������P��λ�ô��ھ�ֹ״̬��ͼ�е������Ϊ��������������| A�� | ��Ƭ��a���ƶ�ʱ����ֻ�����ʾ�������� | |
| B�� | ��Ƭ��a���ƶ�ʱ���ʵ㽫���ϰ��˶� | |
| C�� | ��������S�Ͽ����ʵ㽫���°��˶� | |
| D�� | ��������S�Ͽ���P�㴦���ƽ����� |
�鿴�𰸺ͽ���>>
��Ŀ���������� ��Դ�� ���ͣ�ѡ����
| A�� | λ��һ��Ϊ-x | B�� | ����һ��Ϊp | ||
| C�� | ����һ��ΪEk | D�� | ���ɿ��ܴ���ԭ��״̬ |
�鿴�𰸺ͽ���>>
��Ŀ���������� ��Դ�� ���ͣ���ѡ��
 ��ͼ����������̫������Բ����˶���PΪ���յ㣬QΪԶ�յ㣬M��NΪ�������������˵㣬���е�����ΪT0����ֻ���Ǻ����Ǻ�̫��֮�������ã��������ڴ�P��M��Q��N���˶������У�������
��ͼ����������̫������Բ����˶���PΪ���յ㣬QΪԶ�յ㣬M��NΪ�������������˵㣬���е�����ΪT0����ֻ���Ǻ����Ǻ�̫��֮�������ã��������ڴ�P��M��Q��N���˶������У�������| A�� | ��P��M���õ�ʱ�����$\frac{{T}_{0}}{4}$ | |
| B�� | ��Q��N�Σ���е����� | |
| C�� | ��P��Q�Σ�������С | |
| D�� | ��M��N������������������������������ |
�鿴�𰸺ͽ���>>
��Ŀ���������� ��Դ�� ���ͣ���ѡ��
 ����������0���100���¶��µ�λ���ʼ���ķ�����ռ�ܷ������İٷֱ�������������ʵı仯�ֱ���ͼ������������ʾ������˵����ȷ���ǣ�������
����������0���100���¶��µ�λ���ʼ���ķ�����ռ�ܷ������İٷֱ�������������ʵı仯�ֱ���ͼ������������ʾ������˵����ȷ���ǣ�������| A�� | ͼ������������������ | |
| B�� | ͼ�����߶�Ӧ����������ƽ�����ܽ�С������ | |
| C�� | ͼ��ʵ�߶�Ӧ������������100��ʱ������ | |
| D�� | ͼ�����߸����������������������������Ŀ | |
| E�� | ��0��ʱ��ȣ�100��ʱ�����������ʳ�����0��400 m/s�����ڵķ�����ռ�ܷ������İٷֱȽϴ� |
�鿴�𰸺ͽ���>>
��Ŀ���������� ��Դ�� ���ͣ�ѡ����
| A�� | $\frac{{\sqrt{{k^2}-1}}}{k}$ | B�� | $\frac{{\sqrt{{k^2}+1}}}{k}$ | C�� | $\frac{k}{{\sqrt{{k^2}-1}}}$ | D�� | $\frac{1}{{\sqrt{1-{k^2}}}}$ |
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com