
分析 (1)在星球表面重力与万有引力相等求得重力加速度的表达式,由表达式根据星球半径与地球半径质量与地球质量的关系求得重力加速度的比值即可;
(2)根据万有引力提供圆周运动向心力求得中心球体的质量与环绕天体的半径和周期的关系求解中心天体的质量关系.
解答 解:设行星的质量和半径分别为m1、R1,地球的质量和半径分别为m2、R2;行星绕红矮星运动的轨道半径和周期分别为r1、T1,地球绕太阳公转的半径和周期分别为r2、T2.
(1)在星球表面重力与万有引力相等有:$G\frac{mM}{{R}^{2}}=mg$,可得星球表面重力加速度$g=\frac{GM}{R}$
所以$\frac{{g}_{1}}{{g}_{2}}=\frac{G\frac{{m}_{1}}{{R}_{1}^{2}}}{G\frac{{m}_{2}}{{R}_{2}^{2}}}=\frac{{m}_{1}}{{m}_{2}}•(\frac{{R}_{2}}{{R}_{1}})^{2}$=$\frac{6}{1}×(\frac{1}{2})^{2}$=$\frac{3}{2}$
(2)环绕天体围绕中心天体圆周运动时万有引力提供圆周运动向心力有:
$G\frac{mM}{{r}^{2}}=mr\frac{4{π}^{2}}{{T}^{2}}$
可得中心天体质量M=$\frac{4{π}^{2}{r}^{3}}{G{T}^{2}}$
所以有:$\frac{{M}_{1}}{{M}_{2}}=\frac{\frac{4{π}^{2}{r}_{1}^{3}}{G{T}_{1}^{2}}}{\frac{4{π}^{2}{r}_{2}^{3}}{G{T}_{2}^{2}}}=(\frac{{r}_{1}}{{r}_{2}})^{3}•(\frac{{T}_{2}}{{T}_{1}})^{2}$=$(\frac{\frac{1}{50}}{1})^{3}×(\frac{1}{\frac{1}{200}})^{2}$=$\frac{8}{25}$
答:(1)g1和g2的比值约为3:2;
(2)M1和M2的比值约为8:25.
点评 万有引力的应用主要成以下两方面入手:一是不考虑星球自转的情况下万有引力与星球表面的重力大小相等;二是万有引力提供环绕天体圆周运动的向心力.


科目:高中物理 来源: 题型:填空题

查看答案和解析>>
科目:高中物理 来源: 题型:填空题
查看答案和解析>>
科目:高中物理 来源: 题型:选择题
 2011年9月29日,我国成功发射“天宫一号”目标飞行器,“天宫一号”实际上是空间实验室的实验版.之后,我国将发射“神舟八号”飞船并与“天宫一号”实现对接.某同学画出“天宫一号”和“神舟八号”绕地球做匀速圆周运动的假想图,如图所示,A代表“天宫一号”,B代表“神舟八号”,虚线为各自的轨道.由此假想图,可以判定( )
2011年9月29日,我国成功发射“天宫一号”目标飞行器,“天宫一号”实际上是空间实验室的实验版.之后,我国将发射“神舟八号”飞船并与“天宫一号”实现对接.某同学画出“天宫一号”和“神舟八号”绕地球做匀速圆周运动的假想图,如图所示,A代表“天宫一号”,B代表“神舟八号”,虚线为各自的轨道.由此假想图,可以判定( )| A. | “天宫一号”的运行速率大于“神舟八号”的运行速率 | |
| B. | “天宫一号”的周期小于“神舟八号”的周期 | |
| C. | “天宫一号”的向心加速度大于“神舟八号”的向心加速度 | |
| D. | “神舟八号”适度加速就可以实现与“天宫一号”对接 |
查看答案和解析>>
科目:高中物理 来源: 题型:多选题
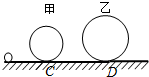 在水平地面上,有如图所示的装置,半径分别为r和R(R>r)的甲、乙两个光滑的圆形轨道安置在同一竖直平面上,轨道之间有一条水平轨道CD相通.让一小球以一定的初速先滑上甲轨道,通过粗糙的CD段,又滑上乙轨道,最后离开两圆轨道.下列说法正确的是( )
在水平地面上,有如图所示的装置,半径分别为r和R(R>r)的甲、乙两个光滑的圆形轨道安置在同一竖直平面上,轨道之间有一条水平轨道CD相通.让一小球以一定的初速先滑上甲轨道,通过粗糙的CD段,又滑上乙轨道,最后离开两圆轨道.下列说法正确的是( )| A. | 小球最后离开两圆轨道时的速度小于滑上甲轨道时的初速度 | |
| B. | 小球经过甲轨道最高点时比经过乙轨道最高点时速度大 | |
| C. | 小球经过甲、乙轨道最低点时对轨道的压力相等 | |
| D. | 小球经过甲、乙轨道最高点时对轨道的压力相等 |
查看答案和解析>>
科目:高中物理 来源: 题型:解答题

查看答案和解析>>
科目:高中物理 来源: 题型:解答题
 如图所示,直角坐标系的x轴沿水平方向,y轴沿竖直方向,在y>0的区域中有竖直向下的匀强电场E1,在第四象限存在竖直向上的匀强电场E2和垂直于xoy平面、水平向外的匀强磁场B,一质量为m,电荷量+q的带电质点,以v0的初速度从第二象限内的A点(-2h,2h)水平抛出,经过x轴上的P点(2h,0)进入第四象限,在第四象限内恰好做匀速圆周运动,且运动半周后进入第三象限.已知重力加速度为g,求:
如图所示,直角坐标系的x轴沿水平方向,y轴沿竖直方向,在y>0的区域中有竖直向下的匀强电场E1,在第四象限存在竖直向上的匀强电场E2和垂直于xoy平面、水平向外的匀强磁场B,一质量为m,电荷量+q的带电质点,以v0的初速度从第二象限内的A点(-2h,2h)水平抛出,经过x轴上的P点(2h,0)进入第四象限,在第四象限内恰好做匀速圆周运动,且运动半周后进入第三象限.已知重力加速度为g,求:查看答案和解析>>
科目:高中物理 来源: 题型:解答题
 如图所示,一轻弹簧两端分别连接物体a,b.
如图所示,一轻弹簧两端分别连接物体a,b.查看答案和解析>>
科目:高中物理 来源: 题型:多选题
| A. | 匀速直线运动 | B. | 匀加速直线运动 | C. | 匀减速直线运动 | D. | 静止 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com