
(25分)普通光纤是一种可传输光的圆柱形细丝,由具有圆形截面的纤芯![]() 和包层
和包层![]() 组成,
组成,![]() 的折射率小于
的折射率小于![]() 的折射率,光纤的端面和圆柱体的轴垂直,由一端面射入的光在很长的光纤中传播时,在纤芯
的折射率,光纤的端面和圆柱体的轴垂直,由一端面射入的光在很长的光纤中传播时,在纤芯![]() 和包层
和包层![]() 的分界面上发生多次全反射.现在利用普通光纤测量流体
的分界面上发生多次全反射.现在利用普通光纤测量流体![]() 的折射率.实验方法如下:让光纤的一端(出射端)浸在流体
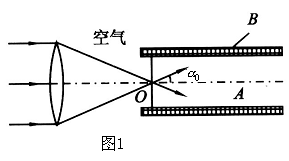
的折射率.实验方法如下:让光纤的一端(出射端)浸在流体![]() 中.令与光纤轴平行的单色平行光束经凸透镜折射后会聚光纤入射端面的中心
中.令与光纤轴平行的单色平行光束经凸透镜折射后会聚光纤入射端面的中心![]() ,经端面折射进入光纤,在光纤中传播.由点
,经端面折射进入光纤,在光纤中传播.由点![]() 出发的光束为圆锥形,已知其边缘光线和轴的夹角为
出发的光束为圆锥形,已知其边缘光线和轴的夹角为![]() ,如图1所示.最后光从另一端面出射进入流体
,如图1所示.最后光从另一端面出射进入流体![]() .在距出射端面
.在距出射端面![]() 处放置一垂直于光纤轴的毛玻璃屏
处放置一垂直于光纤轴的毛玻璃屏![]() ,在
,在![]() 上出现一圆形光斑,测出其直径为
上出现一圆形光斑,测出其直径为![]() ,然后移动光屏
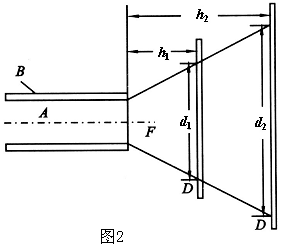
,然后移动光屏![]() 至距光纤出射端面
至距光纤出射端面![]() 处,再测出圆形光斑的直径
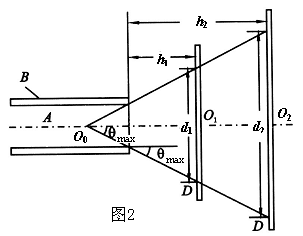
处,再测出圆形光斑的直径![]() ,如图2所示.
,如图2所示.
1.若已知![]() 和
和![]() 的折射率分别为
的折射率分别为![]() 与
与![]() ,求被测流体
,求被测流体![]() 的折射率
的折射率![]() 的表达式.
的表达式.
2.若![]() 、
、![]() 和
和![]() 均为未知量,如何通过进一步的实验以测出
均为未知量,如何通过进一步的实验以测出![]() 的值?
的值?
解析:
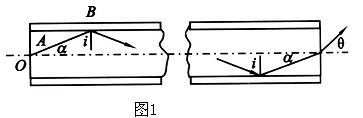
1.由于光纤内所有光线都从轴上的![]() 点出发,在光纤中传播的光线都与轴相交,位于通过轴的纵剖面内,图1为纵剖面内的光路图,设由
点出发,在光纤中传播的光线都与轴相交,位于通过轴的纵剖面内,图1为纵剖面内的光路图,设由![]() 点发出的与轴的夹角为
点发出的与轴的夹角为![]() 的光线,射至
的光线,射至![]() 、
、![]() 分界面的入射角为
分界面的入射角为![]() ,反射角也为
,反射角也为![]() .该光线在光纤中多次反射时的入射角均为
.该光线在光纤中多次反射时的入射角均为![]() ,射至出射端面时的入射角为
,射至出射端面时的入射角为![]() .若该光线折射后的折射角为
.若该光线折射后的折射角为![]() ,则由几何关系和折射定律可得
,则由几何关系和折射定律可得
![]() (1)
(1)
![]() (2)
(2)
当![]() 大于全反射临界角
大于全反射临界角![]() 时将发生全反射,没有光能损失,相应的光线将以不变的光强射向出射端面,而
时将发生全反射,没有光能损失,相应的光线将以不变的光强射向出射端面,而![]() 的光线则因在发生反射时有部分光线通过折射进入
的光线则因在发生反射时有部分光线通过折射进入![]() ,反射光强随着反射次数的增大而越来越弱,以致在未到达出射端面之前就已经衰减为零了.因而能射向出射端面的光线的
,反射光强随着反射次数的增大而越来越弱,以致在未到达出射端面之前就已经衰减为零了.因而能射向出射端面的光线的![]() 的数值一定大于或等于
的数值一定大于或等于![]() ,
,![]() 的值由下式决定
的值由下式决定
![]() (3)
(3)
与![]() 对应的
对应的![]() 值为
值为
![]() (4)
(4)
当![]() 时,即
时,即![]() 时,或
时,或![]() 时,由
时,由![]() 发出的光束中,只有
发出的光束中,只有![]() 的光线才满足
的光线才满足![]() 的条件,才能射向端面,此时出射端面处
的条件,才能射向端面,此时出射端面处![]() 的最大值为
的最大值为
![]() (5)
(5)
若![]() ,即
,即![]() 时,则由
时,则由![]() 发出的光线都能满足
发出的光线都能满足![]() 的条件,因而都能射向端面,此时出射端面处
的条件,因而都能射向端面,此时出射端面处![]() 的最大值为
的最大值为
![]() (6)
(6)
端面处入射角![]() 最大时,折射角
最大时,折射角![]() 也达最大值,设为
也达最大值,设为![]() ,由(2)式可知
,由(2)式可知
![]() (7)
(7)
由(6)、(7)式可得,当![]() 时
时
![]() (8)
(8)
由(3)至(7)式可得,当![]() 时
时
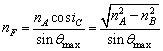 (9)
(9)
![]() 的数值可由图2上的几何关系求得
的数值可由图2上的几何关系求得
 (10)
(10)
于是![]() 的表达式应为
的表达式应为
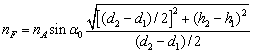 (
(![]() ) (11)
) (11)
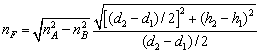 (
(![]() ) (12)
) (12)
2. 可将输出端介质改为空气,光源保持不变,按同样手续再做一次测量,可测得![]() 、
、![]() 、
、![]() 、
、![]() ,这里打撇的量与前面未打撇的量意义相同.已知空气的折射率等于1,故有
,这里打撇的量与前面未打撇的量意义相同.已知空气的折射率等于1,故有
当![]() 时
时 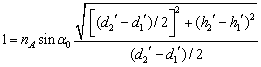 (13)
(13)
当![]() 时
时 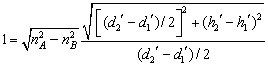 (14)
(14)
将(11)、(12)两式分别与(13)、(14)相除,均得
 (15)
(15)
这结果适用于![]() 为任何值的情况。
为任何值的情况。
评分标准:本题25分
1. 18分。(8)式、(9)式各6分,求得(11)式、(12)式再各给3分
2. 7分。(13)式、(14)式各2分,求得(15)式再给3分。如果利用已知其折射率的液体代替空气,结果正确,照样给分。


 培优好卷单元加期末卷系列答案
培优好卷单元加期末卷系列答案 一线名师权威作业本系列答案
一线名师权威作业本系列答案湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com