
| A. | $\sqrt{2}$ | B. | $\root{3}{2}$ | C. | 2 | D. | $\root{3}{4}$ |
分析 在四颗星组成的四星系统中,其中任意一颗星受到其它三颗星对它的合力提供圆周运动的向心力,根据合力提供向心力,求出正方形的边长和原来的边长的比值
解答 解:设原来正方形的边长为${l}_{1}^{\;}$,角速度为${ω}_{1}^{\;}$,后来正方形的边长变为${l}_{2}^{\;}$,角速度为${ω}_{2}^{\;}$,则有
$2G\frac{{m}_{\;}^{2}}{{l}_{1}^{2}}cos45°+G\frac{{m}_{\;}^{2}}{(\sqrt{2}{l}_{1}^{\;})_{\;}^{2}}=m{ω}_{1}^{2}(\frac{\sqrt{2}}{2}{l}_{1}^{\;})$①
$2G\frac{{m}_{\;}^{2}}{{l}_{2}^{2}}cos45°+G\frac{{m}_{\;}^{2}}{(\sqrt{2}{l}_{2}^{\;})_{\;}^{2}}=m{ω}_{2}^{2}(\frac{\sqrt{2}}{2}{l}_{2}^{\;})$②
周期变为原来2倍,角速度为原来$\frac{1}{2}$,即$\frac{(\;\;\;\;)}{(\;\;\;\;)}\frac{{ω}_{2}^{\;}}{{ω}_{1}^{\;}}=\frac{1}{2}$③
联立解得:$\frac{{l}_{2}^{\;}}{{l}_{1}^{\;}}=\root{3}{4}$,选项D正确,ABC错误
故选:D
点评 解决本题的关键掌握万有引力等于重力,以及知道在四颗星组成的四星系统中,其中任意一颗星受到其它三颗星对它的合力提供圆周运动的向心力.


 阅读快车系列答案
阅读快车系列答案科目:高中物理 来源: 题型:解答题
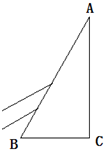 如图所示,一束宽为$\frac{L}{12}$的平行可见光,包含有两种色光,从空气射入顶角为30度的直角透明砖,砖底边长为L,若透明砖对其中一种色光的折射率的折射率n1=$\sqrt{3}$,对另一种色光的折射率为n2<$\sqrt{3}$,当色光上部从AB面中点以60度入射角入射,使这两种色光恰能在透明砖AC表面处射出时分开,则折射率n2至少应为多少?(结果可用反三角函数表示)
如图所示,一束宽为$\frac{L}{12}$的平行可见光,包含有两种色光,从空气射入顶角为30度的直角透明砖,砖底边长为L,若透明砖对其中一种色光的折射率的折射率n1=$\sqrt{3}$,对另一种色光的折射率为n2<$\sqrt{3}$,当色光上部从AB面中点以60度入射角入射,使这两种色光恰能在透明砖AC表面处射出时分开,则折射率n2至少应为多少?(结果可用反三角函数表示)查看答案和解析>>
科目:高中物理 来源: 题型:选择题
 一物体受到如图所示的F1、F2作用,且已知F1、F2互相垂直,大小分别为6N和8N,则该物体受到F1、F2的合力大小是( )
一物体受到如图所示的F1、F2作用,且已知F1、F2互相垂直,大小分别为6N和8N,则该物体受到F1、F2的合力大小是( )| A. | 2N | B. | 6N | C. | 10N | D. | 14N |
查看答案和解析>>
科目:高中物理 来源: 题型:解答题
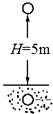 如图,一质量为m=2kg的铅球从离地面H=5m高处自由下落,陷入泥潭中某处后静止不动,整个过程共用时t=1.1s,g取10m/s2.求:
如图,一质量为m=2kg的铅球从离地面H=5m高处自由下落,陷入泥潭中某处后静止不动,整个过程共用时t=1.1s,g取10m/s2.求:查看答案和解析>>
科目:高中物理 来源: 题型:选择题
| A. | 气体体积指的是该气体所有分子能到达的空间的体积,而不是该气体所有分子体积之和 | |
| B. | 气体分子热运动的剧烈程度增强时,气体的温度可能降低 | |
| C. | 外界对气体做功时,其内能不可能会减少 | |
| D. | 在完全失重的情况下,气体对容器壁的压强为零 |
查看答案和解析>>
科目:高中物理 来源: 题型:计算题
查看答案和解析>>
科目:高中物理 来源: 题型:计算题
 如图所示,轻弹簧的一段固定,另一端与一质量为M=1.99kg的物块相连,开始时弹簧处于原长,现有一质量为m=0.01kg的子弹以v0=600m/s的水平速度射向物块,并留在物块中一起向左运动,经过时间t=0.3s后停下,此时弹簧的压缩量x=20cm.已知物块与地面之间的动摩擦因数μ=0.5,重力加速度g取10m/s2,求:
如图所示,轻弹簧的一段固定,另一端与一质量为M=1.99kg的物块相连,开始时弹簧处于原长,现有一质量为m=0.01kg的子弹以v0=600m/s的水平速度射向物块,并留在物块中一起向左运动,经过时间t=0.3s后停下,此时弹簧的压缩量x=20cm.已知物块与地面之间的动摩擦因数μ=0.5,重力加速度g取10m/s2,求:查看答案和解析>>
科目:高中物理 来源: 题型:解答题
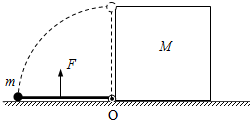 如图所示,长为L的轻杆一端连着质量为m的小球,另一端用活动铰链固接于水平地面上的O点,初始时小球静止于地面上,边长为L、质量为M的正方体左侧静止于O点处.现在杆中点处施加一大小始终为$\frac{6mg}{π}$(g为重力加速度)、方向始终垂直杆的拉力,经过一段时间后撤去F,小球恰好能到达最高点.忽略一切摩擦,试求:
如图所示,长为L的轻杆一端连着质量为m的小球,另一端用活动铰链固接于水平地面上的O点,初始时小球静止于地面上,边长为L、质量为M的正方体左侧静止于O点处.现在杆中点处施加一大小始终为$\frac{6mg}{π}$(g为重力加速度)、方向始终垂直杆的拉力,经过一段时间后撤去F,小球恰好能到达最高点.忽略一切摩擦,试求:查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com