
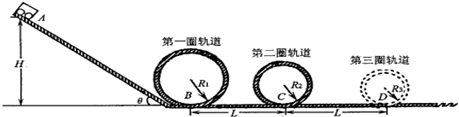
 过山车是游乐场中常见的设施,如图是一种过山车的简易模型.它由水平轨道和在竖直平面内的若干个光滑圆形轨道组成,A、B、C…分别是各个圆形轨道的最低点,第一圆轨道的半径R1=2.0m,以后各个圆轨道半径均是前一轨道半径的k倍(k=0.8),相邻两最低点间的距离为两点所在圆的半径之和.一个质量m=1.0kg的物块(视为质点),从第一圆轨道的左侧沿轨道向右运动,经过A点时的速度大小为v0=12m/s.已知水平轨道与物块间的动摩擦因数μ=0.5,水平轨道与圆弧轨道平滑连接. g取10m/s2,lg0.45=-0.347,lg0.8=-0.097.试求:
过山车是游乐场中常见的设施,如图是一种过山车的简易模型.它由水平轨道和在竖直平面内的若干个光滑圆形轨道组成,A、B、C…分别是各个圆形轨道的最低点,第一圆轨道的半径R1=2.0m,以后各个圆轨道半径均是前一轨道半径的k倍(k=0.8),相邻两最低点间的距离为两点所在圆的半径之和.一个质量m=1.0kg的物块(视为质点),从第一圆轨道的左侧沿轨道向右运动,经过A点时的速度大小为v0=12m/s.已知水平轨道与物块间的动摩擦因数μ=0.5,水平轨道与圆弧轨道平滑连接. g取10m/s2,lg0.45=-0.347,lg0.8=-0.097.试求:| gRn |
| 1 |
| 2 |
| v | 2 0 |
| 1 |
| 2 |
|
| 122-4×10×2 |
| 1 |
| 2 |
| v | 2 B |
| 1 |
| 2 |
| v | 2 0 |
| ||
| R2 |
| ||
| R2 |
| 122-2×0.5×10×(2+1.6) |
| 1.6 |
| ||
| Rn |
| 1 |
| 2 |
| v | 2 n |
| 1 |
| 2 |
| v | 2 0 |
| v | 2 0 |
| R1(1-kn-1) |
| 1-k |
| R2(1-kn-1) |
| 1-k |
| v | 2 0 |
| (1+k)(1-kn-1) |
| 1-k |
| lg0.45 |
| lg0.8 |


科目:高中物理 来源: 题型:

查看答案和解析>>
科目:高中物理 来源: 题型:
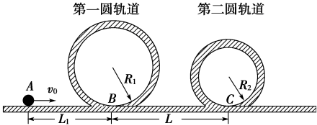 是一种过山车的简易模型,它由水平轨道和在竖直平面内的两个圆形轨道组成,C、D分别是两个圆形轨道的最低点,A、C间距与C、D问距相等,半径R1=1.4m.一个质量为m=1.0kg的小球(视为质点),从轨道的左侧A点以v0=2
是一种过山车的简易模型,它由水平轨道和在竖直平面内的两个圆形轨道组成,C、D分别是两个圆形轨道的最低点,A、C间距与C、D问距相等,半径R1=1.4m.一个质量为m=1.0kg的小球(视为质点),从轨道的左侧A点以v0=2| 30 |
查看答案和解析>>
科目:高中物理 来源: 题型:
查看答案和解析>>
科目:高中物理 来源: 题型:
 过山车是游乐场中常见的设施.如图是一种过山车的简易模型,它由水平轨道和在竖直平面内半径R=2.0m的圆形轨道组成,B、C分别是圆形轨道的最低点和最高点.一个质量为m=1.0kg的小滑块(可视为质点),从轨道的左侧A点以v0=12m/s的初速度沿轨道向右运动,A、B间距L=11.5m.小滑块与水平轨道间的动摩擦因数μ=0.10.圆形轨道是光滑的,水平轨道足够长.取重力加速度g=10m/s2.求:
过山车是游乐场中常见的设施.如图是一种过山车的简易模型,它由水平轨道和在竖直平面内半径R=2.0m的圆形轨道组成,B、C分别是圆形轨道的最低点和最高点.一个质量为m=1.0kg的小滑块(可视为质点),从轨道的左侧A点以v0=12m/s的初速度沿轨道向右运动,A、B间距L=11.5m.小滑块与水平轨道间的动摩擦因数μ=0.10.圆形轨道是光滑的,水平轨道足够长.取重力加速度g=10m/s2.求:查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com