
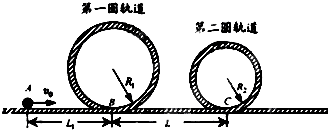
 过山车是游乐场中常见的设施.如图是一种过山车的简易模型,它由粗糙的水平轨道和在竖直平面内的两个光滑圆形轨道组成,B、C分别是两个圆形轨道的最低点,第一个圆形轨道的半径R1=1.4m.一个质量为m=1.0kg的小球(视为质点),从轨道的左侧A点以v0=12.0m/s的初速度沿轨道向右运动,恰能通过第一圆轨道的最高点A、B间距L1=18.5m,B、C间距L2=12.5m.假设水平轨道足够长,圆形轨道间不相互重叠.重力加速度取g=10m/s2,计算结果保留小数点后一位数字.试求
过山车是游乐场中常见的设施.如图是一种过山车的简易模型,它由粗糙的水平轨道和在竖直平面内的两个光滑圆形轨道组成,B、C分别是两个圆形轨道的最低点,第一个圆形轨道的半径R1=1.4m.一个质量为m=1.0kg的小球(视为质点),从轨道的左侧A点以v0=12.0m/s的初速度沿轨道向右运动,恰能通过第一圆轨道的最高点A、B间距L1=18.5m,B、C间距L2=12.5m.假设水平轨道足够长,圆形轨道间不相互重叠.重力加速度取g=10m/s2,计算结果保留小数点后一位数字.试求分析 (1)小球恰能通过第一圆轨道的最高点,在最高点时,由重力提供向心力,由牛顿第二定律求小球在经过第一圆轨道最高点时的速度大小.
(2)小球从开始到运动到第一圆轨道运动最高点的过程,运用动能定理可求得小球与水平轨道间的动摩擦因数.
(3)要保证小球不脱离轨道,有两种情况:
I.轨道半径较小时,小球恰能通过第二个圆轨道,与上题相似,根据牛顿第二定律求出小球通过最高点时的速度,根据动能定理求解半径R2.
II.轨道半径较大时,小球上升的最大高度等于R2,即上升到与圆心等高处,根据动能定理求解半径R2.为保证圆形轨道间不相互重叠,根据几何知识知:R2最大值应满足:(R1+R2)2=L2+(R1-R2)2,解得R2.即可得到半径R2的可变范围;根据动能定理求解小球最终停留点与起始点A的距离.
解答 解:(1)设小球在经过第一圆轨道最高点时的速度大小为v1.
小球在最高点时,由重力提供向心力,由牛顿第二定律得
mg=m$\frac{{v}_{1}^{2}}{{R}_{1}}$
解得 v1=$\sqrt{14}$m/s
(2)小球从开始到运动到第一圆轨道运动最高点的过程,由动能定理得:
-μmgL1-2mgR1=$\frac{1}{2}m{v}_{1}^{2}$-$\frac{1}{2}m{v}_{0}^{2}$
解得 μ=0.2
(3)要保证小球不脱离轨道,可分两种情况进行讨论:
I.轨道半径较小时,小球恰能通过第二个圆轨道,设在最高点的速度为v2,应满足
mg=m$\frac{{v}_{2}^{2}}{{R}_{2}}$
从A到第二圆轨道最高点的过程,由动能定理得
-μmg(L1+L2)-2mgR2=$\frac{1}{2}$mv22-$\frac{1}{2}$v02
由上两式解得:R2=0.4m
II.轨道半径较大时,小球上升的最大高度为R2,即上升到与圆心等高的位置,
根据动能定理得
-μmg(L1+L)-mgR2=0-$\frac{1}{2}$mv02
解得:R2=1.0m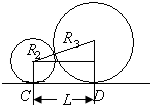
为了保证圆轨道不重叠,R2最大值应满足:(R1+R2)2=L2+(R1-R2)2,
解得 R2=27.9m
综合I、II,要使小球不脱离轨道,则第三个圆轨道的半径须满足下面的条件
0<R2≤0.4m 或 1.0m≤R2≤27.9m
当0<R2≤0.4m 时,小球最终停留点与起始点A的距离为L′,则
-μmgL′=0-$\frac{1}{2}$mv02
解得 L′=36.0m
当1.0m≤R2≤27.9m 时,小球最终停留点与起始点A的距离为L〞,则
L″=L′-2(L′-L1-L)=36-2×(36-18.5-12.5)=26.0m
答:
(1)小球在经过第一圆轨道最高点时的速度大小是3.7m/s;
(2)小球与水平轨道间的动摩擦因数是0.2;
(3)如果要使小球不能脱离轨道,在第二个圆形轨道的设计中,半径R2的可变范围为 0<R2≤0.4m 或 1.0m≤R2≤27.9m;小球最终停留点与起点A的距离是36.0m或26.0m.
点评 选取研究过程,运用动能定理解题.动能定理的优点在于适用任何运动包括曲线运动.知道小球恰能通过圆形轨道的含义:重力等于向心力.要知道使小球不能脱离轨道并不一定要求做完整的圆周运动.


科目:高中物理 来源: 题型:实验题
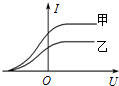 用频率为v但强度不同的甲乙两种光做光电效应实验,发现光电流与电压的关系如图所示,由图可知,甲(选填甲或乙)光的强度大.已知普朗克常量为h,被照射金属的逸出功为W0,则光电子的最大初动能为hγ-W0.
用频率为v但强度不同的甲乙两种光做光电效应实验,发现光电流与电压的关系如图所示,由图可知,甲(选填甲或乙)光的强度大.已知普朗克常量为h,被照射金属的逸出功为W0,则光电子的最大初动能为hγ-W0.查看答案和解析>>
科目:高中物理 来源: 题型:多选题
| A. | 因为液体表面层分子分布比内部稀疏,因此液体表面有收缩趋势 | |
| B. | 当分子力表现为引力时,分子势能随分子间距离的减小而增大 | |
| C. | 第二类永动机不可能制成,因为它违背能量守恒定律 | |
| D. | 一定质量的理想气体,当它的压强、体积都增大时,其内能一定增加 | |
| E. | 水的饱和汽压随温度的升高而减小 |
查看答案和解析>>
科目:高中物理 来源: 题型:多选题

| A. | 电压表的示数为6 V | |
| B. | 在t=0.005 s时,穿过线圈的磁通量为最大 | |
| C. | 若线圈的转速改为25 r/s,则电动势的有效值为3 V | |
| D. | 若线圈的转速改为25 r/s,则通过电灯的电流为0.3 A |
查看答案和解析>>
科目:高中物理 来源: 题型:实验题
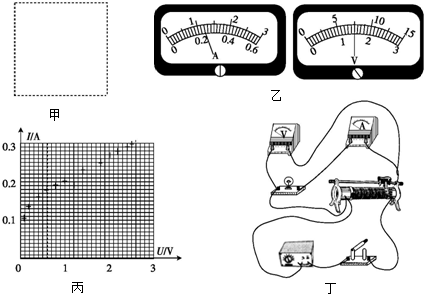
查看答案和解析>>
科目:高中物理 来源: 题型:填空题
查看答案和解析>>
科目:高中物理 来源: 题型:多选题
| A. | 丹麦物理学家奥斯特发现了电磁感应现象 | |
| B. | 英国物理学家法拉弟发现了电流周围存在磁场 | |
| C. | 法国物理学家安培用分子电流假说解释了磁体产生磁场的原因 | |
| D. | 荷兰物理学家惠更斯提出了惠更斯原理,解释了波的反射和折射现象 |
查看答案和解析>>
科目:高中物理 来源: 题型:解答题
查看答案和解析>>
科目:高中物理 来源: 题型:选择题
| A. | ${\;}_{7}^{14}$N+${\;}_{2}^{4}$He→${\;}_{8}^{17}$O+${\;}_{1}^{1}$H | B. | ${\;}_{92}^{238}$U→${\;}_{90}^{234}$Th+${\;}_{2}^{4}$He | ||
| C. | ${\;}_{1}^{2}$H+${\;}_{1}^{3}$H→${\;}_{2}^{4}$He+${\;}_{0}^{1}$n | D. | 4${\;}_{1}^{1}$H→${\;}_{2}^{4}$He+2${\;}_{1}^{0}$e |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com