
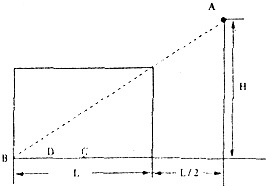
 一个储液桶的底面直径为L.当桶内没有液体时.从桶外某点A恰能看到桶底边缘处的B点,A的高度为H,A距桶边缘的水平距离为
一个储液桶的底面直径为L.当桶内没有液体时.从桶外某点A恰能看到桶底边缘处的B点,A的高度为H,A距桶边缘的水平距离为| L |
| 2 |
| L |
| 2 |
| H |
| 2 |
| H |
| 2 |
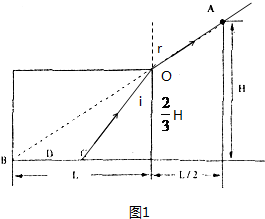
| L | ||||
|
| L | ||||||
2
|
| sinr |
| sini |
| ||
|
| H |
| 2 |
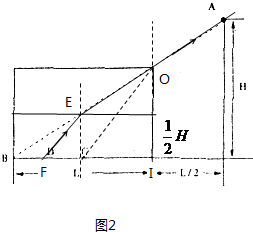
| x1 |
| L |
| ||
|
| x2 | ||
|
| ||
|
| 3 |
| 8 |
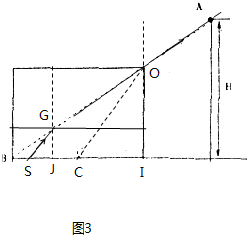
| x3 |
| L |
| h | ||
|
| 3hL |
| 2H |
| x4 | ||
|
| h | ||
|
| 3hL |
| 4H |
| 3hL |
| 4H |
| △x |
| △t |
| ||
| △t |
| 3L |
| 4H |
| h |
| △t |
| h |
| △t |
| △x |
| △t |
| 3L |
| 4H |
| ||
|
| 3 |
| 8 |
| 3L |
| 4H |


湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com