
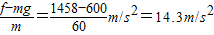
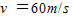
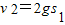
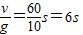 ,
, =
=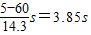 ,
,

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中物理 来源: 题型:

查看答案和解析>>
科目:高中物理 来源: 题型:
查看答案和解析>>
科目:高中物理 来源: 题型:
 某公园计划修建大型游乐设施“翻滚过山车”,设计轨道总长为842m,每车可载28人.游乐过程中过山车将绕半径为5.5m的大圆环回旋,如图所示.若不考虑一切阻力,取g=10m/s2,求:
某公园计划修建大型游乐设施“翻滚过山车”,设计轨道总长为842m,每车可载28人.游乐过程中过山车将绕半径为5.5m的大圆环回旋,如图所示.若不考虑一切阻力,取g=10m/s2,求:查看答案和解析>>
科目:高中物理 来源: 题型:
| ||
| 6 |
查看答案和解析>>
科目:高中物理 来源: 题型:
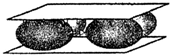 一位质量为60kg的同学为了表演“轻功”,他用打气筒给4只相同的气球充以相等质量的空气(可视为理想气体),然后将这4只气球以相同的方式放在水平放置的木板上,在气球的上方设置一轻质塑料板,如图所示.在这位同学慢慢站上轻质塑料板中间位置的过程中,球内气体温度可视为不变.则下列说法错误的是( )
一位质量为60kg的同学为了表演“轻功”,他用打气筒给4只相同的气球充以相等质量的空气(可视为理想气体),然后将这4只气球以相同的方式放在水平放置的木板上,在气球的上方设置一轻质塑料板,如图所示.在这位同学慢慢站上轻质塑料板中间位置的过程中,球内气体温度可视为不变.则下列说法错误的是( )| A、气体压强是由于气体分子之间的斥力而产生的 | B、气体压强是由于大量气体分子碰撞器壁而产生的 | C、球内气体体积变小 | D、球内气体内能不变 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com