

分析 (1)由粒子做类平抛运动的水平位移和竖直位移求得加速度,进而求得电场强度;
(2)分析粒子运动轨迹,由知道等腰三角形的内底角及腰长求得底边边长,进而求得位置坐标.
解答 (1)带电粒子在第二象限的电场中只受电场力,且电场力方向与初速度方向垂直,所以,粒子做类平抛运动;
粒子从A点到C点用时$t=\frac{OC}{{v}_{0}}=\frac{4}{20}s=\frac{1}{5}s$,;
粒子在水平方向上有$a=\frac{qE}{m}$,所以,$OA=\frac{1}{2}a{t}^{2}$,则有$E=\frac{m}{q}a=\frac{m}{q}\frac{2OA}{{t}^{2}}=\frac{2×2}{100×(\frac{1}{5})^{2}}N/C=1N/C$;
(2)粒子进入磁场时的速度为v,则其竖直分量vy=v0=20m/s,水平分量${v}_{x}=at=\frac{qE}{m}t=20m/s$;
所以,$v=\sqrt{{{v}_{x}}^{2}+{{v}_{y}}^{2}}=20\sqrt{2}m/s$,v与y轴正方向的夹角为45°;
在洛伦兹力作向心力的作用下,$Bvq=\frac{m{v}^{2}}{R}$,粒子在磁场中的做圆周运动的半径$R=\frac{mv}{Bq}=\frac{20\sqrt{2}}{100×0.4}m=\frac{\sqrt{2}}{2}m$;
粒子做圆周运动的周期$T=\frac{2πR}{v}=\frac{π}{20}s$,所以,由图乙可知,粒子每运动半个圆周则偏转方向相反,
则粒子在磁场中的运动如图所示,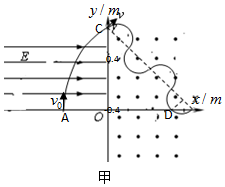 ,
,
因为$4\sqrt{2}=8R$,所以粒子运动第四个半圆的过程中第一次经过x轴,由等腰三角形性质可知,粒子第一、二次经过x轴,在x轴上对应的弦长为$\sqrt{2}r=1m$;
所以OD=3m,则粒子第一次经过x轴时的位置坐标为(3m,0).
答:(1)第二象限内电场的电场强度大小为1N/C;
(2)粒子第一次经过x轴时的位置坐标为(3m,0).
点评 在粒子的运动问题上,要将粒子运动轨迹尽可能画出来以减少问题的难度,如本题若没有画图,则易认为粒子经过4个半圆后第一次与x轴相交.


科目:高中物理 来源: 题型:计算题
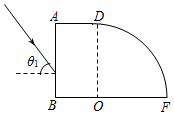 用某种透明材料制成的一块柱体形棱镜的水平截面图如图所示,FD是半径为R的$\frac{1}{4}$圆周,圆心为O,AD长度a=$\frac{1}{2}$R.光线以入射角θ1=60°射到棱镜AB面上,经折射后,光线到达BF面上的O点且恰好不从BF面射出,计算结果可用根式表示.求:
用某种透明材料制成的一块柱体形棱镜的水平截面图如图所示,FD是半径为R的$\frac{1}{4}$圆周,圆心为O,AD长度a=$\frac{1}{2}$R.光线以入射角θ1=60°射到棱镜AB面上,经折射后,光线到达BF面上的O点且恰好不从BF面射出,计算结果可用根式表示.求:查看答案和解析>>
科目:高中物理 来源: 题型:选择题
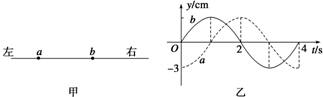
| A. | 波长可能大于3m | B. | 波长可能等于2m | ||
| C. | 波速可能等于$\frac{8}{13}$m/s | D. | 波速可能等于$\frac{2}{7}$m/s |
查看答案和解析>>
科目:高中物理 来源: 题型:多选题
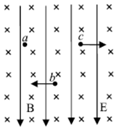 如图所示,匀强电场五竖直向下,匀强磁场5垂直纸面向里.现有三个带有等电量同种电荷的油滴a、b、c,若将它们分别以一定的初速度射入该复合场中,油滴a做勻速圆周运动,油滴b向左水平匀速运动,油滴c向右水平匀速运动,则( )
如图所示,匀强电场五竖直向下,匀强磁场5垂直纸面向里.现有三个带有等电量同种电荷的油滴a、b、c,若将它们分别以一定的初速度射入该复合场中,油滴a做勻速圆周运动,油滴b向左水平匀速运动,油滴c向右水平匀速运动,则( )| A. | 三个油滴可能带正电 | |
| B. | 油滴c所受洛伦兹力方向竖直向上 | |
| C. | 三个油滴质量不一样,b的质量最大 | |
| D. | 油滴a-定是做顺时针方向的圆周运动 |
查看答案和解析>>
科目:高中物理 来源: 题型:多选题
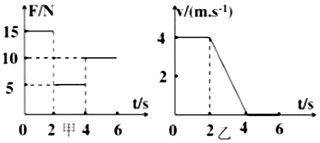 一个物块放置在粗糙的水平面上,受到的水平拉力F随时间t变化的关系如图所示,速度v随时间t变化的关系如图所示(g=10m/s2),下列说法正确的是( )
一个物块放置在粗糙的水平面上,受到的水平拉力F随时间t变化的关系如图所示,速度v随时间t变化的关系如图所示(g=10m/s2),下列说法正确的是( )| A. | 物块的质量为5kg | |
| B. | 5s末物块所受摩擦力的大小15N | |
| C. | 物块在前6s内的位移大小12m | |
| D. | 物块与水平地面间的动摩擦因数0.75 |
查看答案和解析>>
科目:高中物理 来源: 题型:多选题
 如图所示,半径为R的圆形区域内有垂直纸面向里的匀强磁场,磁感应强度为B.M为磁场边界上一点,有无数个带电荷量为+q、质量为m的相同粒子(不计重力)在纸面内向各个方向以相同的速率通过M点进入磁场,这些粒子射出边界的位置处于边界的某一段圆弧上,这段圆弧的弧长是圆周长的$\frac{1}{3}$,下列说法中正确的是( )
如图所示,半径为R的圆形区域内有垂直纸面向里的匀强磁场,磁感应强度为B.M为磁场边界上一点,有无数个带电荷量为+q、质量为m的相同粒子(不计重力)在纸面内向各个方向以相同的速率通过M点进入磁场,这些粒子射出边界的位置处于边界的某一段圆弧上,这段圆弧的弧长是圆周长的$\frac{1}{3}$,下列说法中正确的是( )| A. | 粒子从M点进入磁场时的速率为v=$\frac{\sqrt{3}qBR}{2m}$ | |
| B. | 粒子从M点进入磁场时的速率为v=$\frac{qBR}{m}$ | |
| C. | 若将磁感应强度的大小增加到$\sqrt{3}$B,则粒子射出边界的圆弧长度变为原来的$\frac{1}{2}$ | |
| D. | 若将磁感应强度的大小增加到$\frac{\sqrt{6}}{2}$B,则粒子射出边界的圆弧长度变为原来的$\frac{1}{3}$ |
查看答案和解析>>
科目:高中物理 来源: 题型:选择题
| A. | 若飞机从西往东飞,φ1比φ2高 | B. | 若飞机从东往西飞,φ2比φ1高 | ||
| C. | 若飞机从北往南飞,φ1比φ2高 | D. | 若飞机从南往北飞,φ1比φ2高 |
查看答案和解析>>
科目:高中物理 来源: 题型:多选题
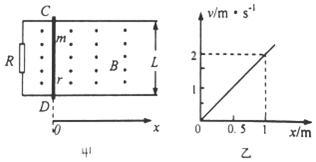 如图甲所示,左侧接有定值电阻R=3Ω的水平粗糙导轨处于垂直纸面向外的匀强磁场中,磁感应强度B=2T,导轨间距L=1m,一质量m=2kg,阻值r=1Ω,金属棒在拉力F作用下由静止开始从CD处沿导轨向右加速运动,金属棒与导轨垂直且接触良好,金属棒与导轨间动摩擦因数μ=0.5,g=10m/s2,金属棒v-x图象如图(乙)所示,则从起点发生x=1m位移的过程中( )
如图甲所示,左侧接有定值电阻R=3Ω的水平粗糙导轨处于垂直纸面向外的匀强磁场中,磁感应强度B=2T,导轨间距L=1m,一质量m=2kg,阻值r=1Ω,金属棒在拉力F作用下由静止开始从CD处沿导轨向右加速运动,金属棒与导轨垂直且接触良好,金属棒与导轨间动摩擦因数μ=0.5,g=10m/s2,金属棒v-x图象如图(乙)所示,则从起点发生x=1m位移的过程中( )| A. | 拉力做的功W=16J | B. | 通过电阻R的感应电量q=0.25C | ||
| C. | 定值电阻R产生的焦耳热为Q=0.75J | D. | 所用的时间t一定大于1s |
查看答案和解析>>
科目:高中物理 来源: 题型:选择题
| A. | 小球线速度大小为2π | B. | 小球角速度大小为2π | ||
| C. | 小球线速度大小为$\frac{π}{2}$ | D. | 小球角速度大小为4π |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com