
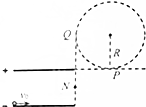
 ��ͼ��ʾ���ռ��д��ڰ뾶ΪR��Բ���н�ų����ų��ķ���ֱֽ�����⣬�Ÿ�Ӧǿ�ȴ�СΪB��ƽ�а��������������Ϊ$\frac{2\sqrt{3}}{3}$R���������ϼ�����ӳ���ǡ����Բ�δų��±߽�������P�㣬�������Ҷ���ֱ������ų���߽�������Q�㣮һ����Ϊm�������Ϊq�Ĵ������ӣ��Դ�СΪ$\frac{BqR}{2m}$�ij��ٶȽ������������ഹֱ�糡�������룬���������Ҷ���ֱ���ߵ��е�N�������ǡ����P������Բ�δų����������ӵ���������
��ͼ��ʾ���ռ��д��ڰ뾶ΪR��Բ���н�ų����ų��ķ���ֱֽ�����⣬�Ÿ�Ӧǿ�ȴ�СΪB��ƽ�а��������������Ϊ$\frac{2\sqrt{3}}{3}$R���������ϼ�����ӳ���ǡ����Բ�δų��±߽�������P�㣬�������Ҷ���ֱ������ų���߽�������Q�㣮һ����Ϊm�������Ϊq�Ĵ������ӣ��Դ�СΪ$\frac{BqR}{2m}$�ij��ٶȽ������������ഹֱ�糡�������룬���������Ҷ���ֱ���ߵ��е�N�������ǡ����P������Բ�δų����������ӵ������������� ��1���������ڵ糡�ʹų�֮��������ֱ���˶��Ĺ켣�õ������뿪�糡ʱ���ٶȷ�������������ڵ糡�����ĩ�ٶȣ�Ȼ������ƽ���˶����ɣ�����λ����õ��Ʋ
��2��������ƽ������������ڵ糡�е��˶�ʱ�䣬��������ֱ���˶�������õ糡���ų�֮����˶�ʱ�䣻�������������������������ð뾶�����ڣ�Ȼ���ɰ뾶������ų����ٶȷ����ݼ��ι�ϵ���ת�������Ľǣ���������˶�ʱ�䣮
��� �⣺��1�������Ӵ�N��������ٶ��뼫��ļн�Ϊ�ȣ�����Ϊd����ͼ��ʾ��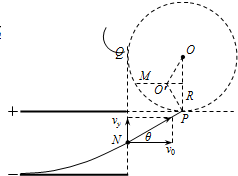 �ɽ�ã�tan��=$\frac{\frac{1}{2}d}{R}$=$\frac{\sqrt{3}}{3}$������=30�㣻
�ɽ�ã�tan��=$\frac{\frac{1}{2}d}{R}$=$\frac{\sqrt{3}}{3}$������=30�㣻
���ԣ�vy=v0tan�ȣ�
�����ڵ糡������ƽ���˶������ӵļ��ٶ�$a=\frac{F}{m}=\frac{qE}{m}=\frac{qU}{md}$����${{v}_{y}}^{2}=ad$=$\frac{qU}{m}$��
���ԣ�$U=\frac{m{{v}_{y}}^{2}}{q}=\frac{m{{v}_{0}}^{2}ta{n}^{2}��}{q}=\frac{{B}^{2}q{R}^{2}}{12m}$��
��2�����������ڵ糡���˶���ʱ��${t}_{1}=\sqrt{\frac{\frac{1}{2}d}{\frac{1}{2}a}}=\sqrt{\frac{d}{a}}=\sqrt{\frac{m{d}^{2}}{qU}}=\sqrt{\frac{16{m}^{2}}{{B}^{2}{q}^{2}}}$=$\frac{4m}{Bq}$��
���������뿪�糡����ų�ǰ������ֱ���˶����˶�ʱ��${t}_{2}=\frac{R}{{v}_{0}}=\frac{2m}{Bq}$��
�������ӽ���ų����ٶ�v=$\frac{{v}_{0}}{cos��}$=$\frac{BqR}{\sqrt{3}m}$��
�����ڴų�����Բ���˶�����������������������qvB=m$\frac{{v}^{2}}{r}$�����ԣ�$r=\frac{mv}{Bq}=\frac{\sqrt{3}}{3}R$��
�ڴų���ƫת�Ĺ켣��ͼ��ʾ����OPO��=30�㣬��POO��=30�㣬���ԣ������ڴų���ת���Ľ�Ϊ360��-2����OPO��+��POO�䣩=240�㣻
���������ڴų�����Բ���˶������ڣ�T=$\frac{2��r}{v}$=$\frac{2��m}{qB}$��
���ԣ������ڴų��е��˶�ʱ��${t}_{3}=\frac{240��}{360��}T=\frac{4��m}{3Bq}$��
���ԣ������������̵��˶�ʱ�䣺$t={t}_{1}+{t}_{2}+{t}_{3}=��\frac{4��}{3}+6��\frac{m}{Bq}$��
�𣺣�1�������������ĵ��Ʋ�Ϊ$\frac{{B}^{2}q{R}^{2}}{12m}$��
��2�����Ӵӽ���糡������ų�������������������ʱ��Ϊ$��\frac{4��}{3}+6��\frac{m}{Bq}$��
���� ���������ڴų����˶���һ��������������������ȡ�ð뾶�����ڣ�Ȼ����ݼ��ι�ϵ�õ��뾶�����Ľǣ��������������⣮



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ���������� ��Դ�� ���ͣ���ѡ��
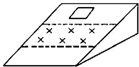 ��ͼ��ʾ���н���ǿ�ų���б�洹ֱ������Ϊm���������߿�ֹ�����Ϊ30��ľ�Եб���ϣ�λ�ڴų��⣩����ʹ�߿����ٶ�v�����˶���ǡ�ô����ų����߿�ı߳�С�ڴų��Ŀ��ȣ��߿���б���Ķ�Ħ������Ϊ��=$\frac{\sqrt{3}}{3}$��������˵����ȷ���ǣ�������
��ͼ��ʾ���н���ǿ�ų���б�洹ֱ������Ϊm���������߿�ֹ�����Ϊ30��ľ�Եб���ϣ�λ�ڴų��⣩����ʹ�߿����ٶ�v�����˶���ǡ�ô����ų����߿�ı߳�С�ڴų��Ŀ��ȣ��߿���б���Ķ�Ħ������Ϊ��=$\frac{\sqrt{3}}{3}$��������˵����ȷ���ǣ�������| A�� | �߿���ȫ����ų����������˶� | |
| B�� | �߿����ų��Ĺ����е������Ĺ����ڴ����ų��Ĺ����е������Ĺ� | |
| C�� | �߿����ʹ����ų�ʱ���ٶȱ仯�����˶���������� | |
| D�� | �߿����ʹ����ų�ʱ���ٶȱ仯�����˶�ʱ������� |
�鿴�𰸺ͽ���>>
��Ŀ���������� ��Դ�� ���ͣ�������
 ��ͼ����һ������Ϊ�ʵ������Ϊm=1kg��С��飬�ӹ⻬ƽ̨���ϵ�A����v0=2m/s �ij��ٶ�ˮƽ�׳�������C��ʱ��ǡ����C�����߷������̶���ˮƽ�����ϵĹ⻬Բ�������OC����ֱ�����60��ǣ����С��黬�Ͻ����⻬Բ�����ĩ��D ������ڹ⻬ˮƽ����������M=3kg���㹻����ľ���ϣ���֪��ľ����С����Ķ�Ħ��������=0.2��Բ���뾶R=0.4m�����ƿ���������gȡ10m/s2����
��ͼ����һ������Ϊ�ʵ������Ϊm=1kg��С��飬�ӹ⻬ƽ̨���ϵ�A����v0=2m/s �ij��ٶ�ˮƽ�׳�������C��ʱ��ǡ����C�����߷������̶���ˮƽ�����ϵĹ⻬Բ�������OC����ֱ�����60��ǣ����С��黬�Ͻ����⻬Բ�����ĩ��D ������ڹ⻬ˮƽ����������M=3kg���㹻����ľ���ϣ���֪��ľ����С����Ķ�Ħ��������=0.2��Բ���뾶R=0.4m�����ƿ���������gȡ10m/s2�����鿴�𰸺ͽ���>>
��Ŀ���������� ��Դ�� ���ͣ���ѡ��
| A�� | ��ͬѧ��Ϊ��vһ��ʱ��rԽ�����hԽ�� | |
| B�� | ��ͬѧ��Ϊ��vһ��ʱ��rԽС���hԽ�� | |
| C�� | ��ͬѧ��Ϊ��rһ��ʱ��vԽС���hԽ�� | |
| D�� | ��ͬѧ��Ϊ��rһ��ʱ��vԽ�����hԽ�� |
�鿴�𰸺ͽ���>>
��Ŀ���������� ��Դ�� ���ͣ�ѡ����
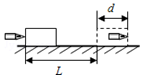 ��ͼ��ʾ��ľ�龲ֹ�ڹ⻬ˮƽ�����ϣ�һ���ӵ�ˮƽ����ľ������Ϊdʱ���ӵ���ľ����Ծ�ֹ�����ӵ�����ľ��Ĺ����У�ľ���������ƶ��ľ���ΪL��ľ����ӵ���ƽ������Ϊf����ô����һ�����У�������
��ͼ��ʾ��ľ�龲ֹ�ڹ⻬ˮƽ�����ϣ�һ���ӵ�ˮƽ����ľ������Ϊdʱ���ӵ���ľ����Ծ�ֹ�����ӵ�����ľ��Ĺ����У�ľ���������ƶ��ľ���ΪL��ľ����ӵ���ƽ������Ϊf����ô����һ�����У�������| A�� | ľ��Ļ�е������fL | |
| B�� | �ӵ��Ļ�е�ܼ�����Ϊfd | |
| C�� | �ӵ���ľ��ϵͳ�Ļ�е�ܱ��ֲ��� | |
| D�� | �ӵ���ľ��ϵͳ�Ļ�е��������mgd |
�鿴�𰸺ͽ���>>
��Ŀ���������� ��Դ�� ���ͣ�ѡ����
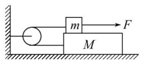 ��ͼ��ʾ��ľ������ΪM������ΪL��Сľ�飨����Ϊ�ʵ㣩������Ϊm��ˮƽ����⻬��һ����������������ͨ�������ֱַ���ľ���Сľ�����ӣ�Сľ����ľ���Ķ�Ħ������Ϊ�̣���ʼʱľ�龲ֹ��ľ����ˣ�����ˮƽ���ҵ�����Сľ������ľ���Ҷˣ�������������Ϊ��������
��ͼ��ʾ��ľ������ΪM������ΪL��Сľ�飨����Ϊ�ʵ㣩������Ϊm��ˮƽ����⻬��һ����������������ͨ�������ֱַ���ľ���Сľ�����ӣ�Сľ����ľ���Ķ�Ħ������Ϊ�̣���ʼʱľ�龲ֹ��ľ����ˣ�����ˮƽ���ҵ�����Сľ������ľ���Ҷˣ�������������Ϊ��������| A�� | 2��mgL | B�� | ��mgL | C�� | �̣�M+m��gL | D�� | $\frac{��mgL}{2}$ |
�鿴�𰸺ͽ���>>
��Ŀ���������� ��Դ�� ���ͣ���ѡ��
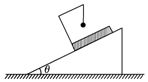 ��ͼ��ʾ��һ����Ϊm1��С��������������������Ϊm2��ľ���֧���ϣ�ľ�������Ϊ�ȵ�б���»�ʱ��ϸ�߳���ֱ״̬����ľ���»��Ĺ�����б����ʼ�վ�ֹ��ˮƽ�����ϣ���֪б���������ΪM���������ٶ�Ϊg��������˵���в���ȷ���ǣ�������
��ͼ��ʾ��һ����Ϊm1��С��������������������Ϊm2��ľ���֧���ϣ�ľ�������Ϊ�ȵ�б���»�ʱ��ϸ�߳���ֱ״̬����ľ���»��Ĺ�����б����ʼ�վ�ֹ��ˮƽ�����ϣ���֪б���������ΪM���������ٶ�Ϊg��������˵���в���ȷ���ǣ�������| A�� | �����б�����֧����С�ڣ�M+m1+m2��g | |
| B�� | ľ����б���Ķ�Ħ������Ϊ$\frac{1}{tan��}$ | |
| C�� | Ħ����������������ľ����ٵĻ�е�� | |
| D�� | б�����ܵ������Ħ����Ϊ�� |
�鿴�𰸺ͽ���>>
��Ŀ���������� ��Դ�� ���ͣ�������
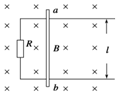 ����ͼ��ʾ��ˮƽ���õ�ƽ�н������죬���l=0.50m����˽�һ����R=1.0�����Ÿ�Ӧǿ��B=1.0T����ǿ�ų�����ֱ�ڵ���ƽ�棬�����ab��ֱ���ڵ����ϣ�������Ħ�����ص��컬��������͵�����ĵ�����ɺ��Բ��ƣ���ab��v=4.0m/s���ٶ�ˮƽ�������ٻ���ʱ����
����ͼ��ʾ��ˮƽ���õ�ƽ�н������죬���l=0.50m����˽�һ����R=1.0�����Ÿ�Ӧǿ��B=1.0T����ǿ�ų�����ֱ�ڵ���ƽ�棬�����ab��ֱ���ڵ����ϣ�������Ħ�����ص��컬��������͵�����ĵ�����ɺ��Բ��ƣ���ab��v=4.0m/s���ٶ�ˮƽ�������ٻ���ʱ�����鿴�𰸺ͽ���>>
��Ŀ���������� ��Դ�� ���ͣ�ѡ����
 ��56���ձ���ش���ϻ�Ϊ������5���Ӽ��ɳ���3000mAh���50%�����Ŀ�似���ɹ�������ҵ��㷺��ע����ͼ�ǻ�Ϊij�����ֻ�����ϵ���Ϣ��֧�ֵ�ѹ�������磬������
��56���ձ���ش���ϻ�Ϊ������5���Ӽ��ɳ���3000mAh���50%�����Ŀ�似���ɹ�������ҵ��㷺��ע����ͼ�ǻ�Ϊij�����ֻ�����ϵ���Ϣ��֧�ֵ�ѹ�������磬������| A�� | 4.35V��ʾ�õ�صĵ綯�� | |
| B�� | 11.4 Wh��ʾ�õ�����ṩ�ĵ��� | |
| C�� | 3000 mAh��ʾ�õ�����ṩ�ĵ��� | |
| D�� | �õ�س�������Ժ���100mA�ĵ�������ʱ������������30Сʱ |
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com