
如图所示,有沿斜向固定的足够长的绝缘管道ab,其倾角为q .管道内有一个质量为m带负电的小圆柱体P,所带电量的绝对值为q.P的横截面直径略小于管道的内径,它与管壁之间的动摩擦因数为m .整个装置处于磁感应强度为B的匀强磁场中,磁场方向垂直管道而远离读者(即垂直纸面向里).小圆柱体P从管道内的顶部由静止释放后将沿管道下滑,试求P下滑的最大速度(设P所带电量保持不变).

本题常见解答为:依题意,带电小圆柱体P释放后将沿管道加速下滑,且受到四个外力,即重力G=mg,管道壁对它的支持力N和滑动摩擦力F=mN,还有洛伦兹力f(其方向由左手定则判断),如图甲所示.当P下滑至做匀速运动时达最大速度,设该速度为vm,相应的洛伦兹力f=qvmB.依据平衡条件可得 平行斜管方向 mgsinq -mN=0 ① 垂直斜管方向 N+qvmB-mgcosq =0 ② 联解①、②两式可得 vm= 先分析带电小圆柱体P沿管道下滑的物理过程的变化情形,大致可分为三个阶段:第一阶段P做的是加速度逐渐增大的变加速运动,其受力情形如图甲所示.P被释放而沿管道下滑时,因其速度的增大,它所受的洛伦兹力(垂直管道向上)随之增大,那么管道下壁(相当于斜面)对它的支持力和相应的摩擦力将逐渐减小直至减为零,显然,在这一阶段中P沿管道下滑的加速度和速度均将逐渐增大.第二阶段P做的是加速度逐渐减小直至为零的变加速运动.当下管壁对P的支持力减至零时,在洛伦兹力的作用下.随即P将贴着上管壁向下滑动,其受力情形如图乙所示.此后上管壁对P的压力(垂直上管壁向下)和摩擦力均将随洛伦兹力的增大而变大,其加速度将逐渐减小直至趋于零(可近似为零),而其速度却仍在增大直至最大.第三阶段P做的是匀速直线运动,其受力情形仍如图乙所示.当P下滑的加速度减为零时,可以认为它将以其最大速度贴着上管壁下滑做匀速直线运动.
乙 可见,本题的常见解答只考虑了带电小圆柱体P在上述物理过程第一阶段的受力情形,且滥用平衡条件列方程.如果磁场方向恰与题设方向相反,相应于P所受的洛伦兹力电该反向即变为垂直管壁向下,那么它开始就将做加速度逐渐减小而速度逐渐增大直至最大的变加速运动,此时上述解答才是对的.对这一物理过程比较简单的情形,学生是较为熟知的,而有的学生却因思维的惰性,不能随机应变,忽略本例物理过程的变化,从而导致失误. 正确解答如下:依上述分析可知,要求出带电小圆柱体P沿斜管下滑的最大速度(设为vm),应选择上述物理过程中的第三个阶段(其受力情形如图乙所示),且依平衡条件列出方程: 平行斜管方向 mgsinq -mN=0 ③ 垂直斜管方向 qvmB-mgcosq -N=0 ④ 联解③、④两式可得 vm= |


 桃李文化快乐暑假武汉出版社系列答案
桃李文化快乐暑假武汉出版社系列答案 优秀生快乐假期每一天全新寒假作业本系列答案
优秀生快乐假期每一天全新寒假作业本系列答案 暑假接力赛新疆青少年出版社系列答案
暑假接力赛新疆青少年出版社系列答案科目:高中物理 来源: 题型:
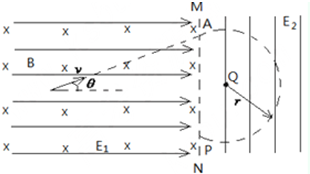 如图所示,虚线MN左侧是水平正交的匀强电场和磁场,电场水平向右,磁场垂直于纸面向里,磁感应强度为B;MN右侧有竖直方向的匀强电场(图中竖线,未标方向),电场中有一固定点电荷Q.一质量为m,电荷量为q的点电荷,从MN左侧的场区沿与电场线成θ角斜向上的匀速直线运动,穿过MN上的A点进入右侧场区,恰好绕Q在竖直面内做半径为r的匀速圆周运动,并穿过MN上的P点进入左侧场区.已知各电场之间无相互影响,当地重力加速度为g,静电力常量为k.
如图所示,虚线MN左侧是水平正交的匀强电场和磁场,电场水平向右,磁场垂直于纸面向里,磁感应强度为B;MN右侧有竖直方向的匀强电场(图中竖线,未标方向),电场中有一固定点电荷Q.一质量为m,电荷量为q的点电荷,从MN左侧的场区沿与电场线成θ角斜向上的匀速直线运动,穿过MN上的A点进入右侧场区,恰好绕Q在竖直面内做半径为r的匀速圆周运动,并穿过MN上的P点进入左侧场区.已知各电场之间无相互影响,当地重力加速度为g,静电力常量为k.查看答案和解析>>
科目:高中物理 来源:不详 题型:问答题
查看答案和解析>>
科目:高中物理 来源:2010-2011学年四川省绵阳市涪城区南山中学高二(下)期中物理试卷(A卷)(解析版) 题型:解答题
查看答案和解析>>
科目:高中物理 来源: 题型:阅读理解
第三部分 运动学
第一讲 基本知识介绍
一. 基本概念
1. 质点
2. 参照物
3. 参照系——固连于参照物上的坐标系(解题时要记住所选的是参照系,而不仅是一个点)
4.绝对运动,相对运动,牵连运动:v绝=v相+v牵
二.运动的描述
1.位置:r=r(t)
2.位移:Δr=r(t+Δt)-r(t)
3.速度:v=limΔt→0Δr/Δt.在大学教材中表述为:v=dr/dt, 表示r对t 求导数
5.以上是运动学中的基本物理量,也就是位移、位移的一阶导数、位移的二阶导数。可是

三阶导数为什么不是呢?因为牛顿第二定律是F=ma,即直接和加速度相联系。(a对t的导数叫“急动度”。)
6.由于以上三个量均为矢量,所以在运算中用分量表示一般比较好
三.等加速运动
v(t)=v0+at r(t)=r0+v0t+1/2 at2

一道经典的物理问题:二次世界大战中物理学家曾经研究,当大炮的位置固定,以同一速度v0沿各种角度发射,问:当飞机在哪一区域飞行之外时,不会有危险?(注:结论是这一区域为一抛物线,此抛物线是所有炮弹抛物线的包络线。此抛物线为在大炮上方h=v2/2g处,以v0平抛物体的轨迹。)
练习题:
一盏灯挂在离地板高l2,天花板下面l1处。灯泡爆裂,所有碎片以同样大小的速度v 朝各个方向飞去。求碎片落到地板上的半径(认为碎片和天花板的碰撞是完全弹性的,即切向速度不变,法向速度反向;碎片和地板的碰撞是完全非弹性的,即碰后静止。)
四.刚体的平动和定轴转动
1. 我们讲过的圆周运动是平动而不是转动
2. 角位移φ=φ(t), 角速度ω=dφ/dt , 角加速度ε=dω/dt
3. 有限的角位移是标量,而极小的角位移是矢量
4. 同一刚体上两点的相对速度和相对加速度
 两点的相对距离不变,相对运动轨迹为圆弧,VA=VB+VAB,在AB连线上
两点的相对距离不变,相对运动轨迹为圆弧,VA=VB+VAB,在AB连线上
投影:[VA]AB=[VB]AB,aA=aB+aAB,aAB=,anAB+,aτAB, ,aτAB垂直于AB,,anAB=VAB2/AB
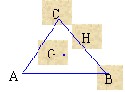
例:A,B,C三质点速度分别VA ,VB ,VC
求G的速度。
五.课后习题:
一只木筏离开河岸,初速度为V,方向垂直于岸边,航行路线如图。经过时间T木筏划到路线上标有符号处。河水速度恒定U用作图法找到在2T,3T,4T时刻木筏在航线上的确切位置。
五、处理问题的一般方法
(1)用微元法求解相关速度问题
例1:如图所示,物体A置于水平面上,A前固定一滑轮B,高台上有一定滑轮D,一根轻绳一端固定在C点,再绕过B、D,BC段水平,当以恒定水平速度v拉绳上的自由端时,A沿水平面前进,求当跨过B的两段绳子的夹角为α时,A的运动速度。
(vA=![]() )
)
(2)抛体运动问题的一般处理方法
(1)将斜上抛运动分解为水平方向的匀速直线运动和竖直方向的竖直上抛运动
(2)将沿斜面和垂直于斜面方向作为x、y轴,分别分解初速度和加速度后用运动学公式解题
(3)将斜抛运动分解为沿初速度方向的斜向上的匀速直线运动和自由落体运动两个分运动,用矢量合成法则求解
例2:在掷铅球时,铅球出手时距地面的高度为h,若出手时的速度为V0,求以何角度掷球时,水平射程最远?最远射程为多少?
(α=![]() 、 x=
、 x=![]() )
)
第二讲 运动的合成与分解、相对运动
(一)知识点点拨

参考系的转换:动参考系,静参考系
相对运动:动点相对于动参考系的运动
绝对运动:动点相对于静参考系统(通常指固定于地面的参考系)的运动
牵连运动:动参考系相对于静参考系的运动
(5)位移合成定理:SA对地=SA对B+SB对地
速度合成定理:V绝对=V相对+V牵连
加速度合成定理:a绝对=a相对+a牵连
(二)典型例题
(1)火车在雨中以30m/s的速度向南行驶,雨滴被风吹向南方,在地球上静止的观察者测得雨滴的径迹与竖直方向成21。角,而坐在火车里乘客看到雨滴的径迹恰好竖直方向。求解雨滴相对于地的运动。
提示:矢量关系入图
答案:83.7m/s
(2)某人手拿一只停表,上了一次固定楼梯,又以不同方式上了两趟自动扶梯,为什么他可以根据测得的数据来计算自动扶梯的台阶数?
提示:V人对梯=n1/t1
V梯对地=n/t2
V人对地=n/t3
V人对地= V人对梯+ V梯对地
答案:n=t2t3n1/(t2-t3)t1

(3)某人驾船从河岸A处出发横渡,如果使船头保持跟河岸垂直的方向航行,则经10min后到达正对岸下游120m的C处,如果他使船逆向上游,保持跟河岸成а角的方向航行,则经过12.5min恰好到达正对岸的B处,求河的宽度。
提示:120=V水*600
D=V船*600
答案:200m
(4)一船在河的正中航行,河宽l=100m,流速u=5m/s,并在距船s=150m的下游形成瀑布,为了使小船靠岸时,不至于被冲进瀑布中,船对水的最小速度为多少?
提示:如图船航行
答案:1.58m/s
(三)同步练习
1.一辆汽车的正面玻璃一次安装成与水平方向倾斜角为β1=30°,另一次安装成倾角为β2=15°。问汽车两次速度之比![]() 为多少时,司机都是看见冰雹都是以竖直方向从车的正面玻璃上弹开?(冰雹相对地面是竖直下落的)
为多少时,司机都是看见冰雹都是以竖直方向从车的正面玻璃上弹开?(冰雹相对地面是竖直下落的)
2、模型飞机以相对空气v=39km/h的速度绕一个边长2km的等边三角形飞行,设风速u = 21km/h ,方向与三角形的一边平行并与飞机起飞方向相同,试求:飞机绕三角形一周需多少时间?
3.图为从两列蒸汽机车上冒出的两股长幅气雾拖尾的照片(俯视)。两列车沿直轨道分别以速度v1=50km/h和v2=70km/h行驶,行驶方向如箭头所示,求风速。
4、细杆AB长L ,两端分别约束在x 、 y轴上运动,(1)试求杆上与A点相距aL(0< a <1)的P点运动轨迹;(2)如果vA为已知,试求P点的x 、 y向分速度vPx和vPy对杆方位角θ的函数。

(四)同步练习提示与答案
1、提示:利用速度合成定理,作速度的矢量三角形。答案为:3。
2、提示:三角形各边的方向为飞机合速度的方向(而非机头的指向);
第二段和第三段![]() 大小相同。
大小相同。
参见右图,显然:
v2 = ![]() + u2 - 2v合ucos120°
+ u2 - 2v合ucos120°
可解出 v合 = 24km/h 。
答案:0.2hour(或12min.)。
3、提示:方法与练习一类似。答案为:3
4、提示:(1)写成参数方程![]() 后消参数θ。
后消参数θ。
(2)解法有讲究:以A端为参照, 则杆上各点只绕A转动。但鉴于杆子的实际运动情形如右图,应有v牵 = vAcosθ,v转 = vA![]() ,可知B端相对A的转动线速度为:v转 + vAsinθ=
,可知B端相对A的转动线速度为:v转 + vAsinθ= ![]() 。
。
P点的线速度必为 ![]() = v相
= v相
所以 vPx = v相cosθ+ vAx ,vPy = vAy - v相sinθ
答案:(1)![]() +
+ ![]() = 1 ,为椭圆;(2)vPx = avActgθ ,vPy =(1 - a)vA
= 1 ,为椭圆;(2)vPx = avActgθ ,vPy =(1 - a)vA
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com