
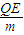
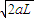 =
=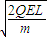 ����ǰB���ٶ�ΪvB1=0������ײ������A��B�����ܶ�������ʧ�������ٶȣ�����ײ��A��B���ٶȷֱ�
����ǰB���ٶ�ΪvB1=0������ײ������A��B�����ܶ�������ʧ�������ٶȣ�����ײ��A��B���ٶȷֱ�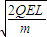 ��
��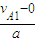 =
=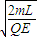
 a��t2-t1��2
a��t2-t1��2 ��
��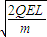 ��
��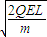 ��
��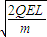 ��
�� a��t3-t2��2������������ײ
a��t3-t2��2������������ײ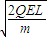 ��
��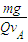 ��A��ļ��ٶ�Ϊ a=
��A��ļ��ٶ�Ϊ a=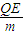
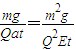 0��t��
0��t��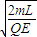
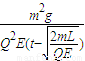
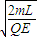 ��t��3
��t��3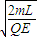
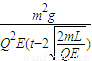 3
3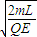 ��t��5
��t��5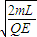
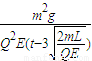 5
5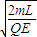 ��t��7
��t��7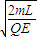
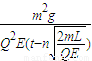 ��2n-1��
��2n-1��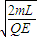 ��t�ܣ�2n+1��
��t�ܣ�2n+1��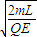 ��n=1��2��3������
��n=1��2��3������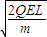 ��
��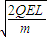 ��
��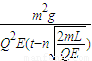 ��2n-1��
��2n-1��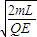 ��t�ܣ�2n+1��
��t�ܣ�2n+1��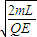 ��n=1��2��3��������
��n=1��2��3��������

 ��У����ϵ�д�
��У����ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ���������� ��Դ�� ���ͣ�
 ��ͼ��ʾ���ڹ⻬��Ե��ˮƽֱ���������������С��a��b��a������Ϊ2m��������Ϊ+q��b������Ϊm��������Ϊ+2q����������Զ�������˶���ijʱ��a��b����ٶȴ�С����Ϊv��1.5v�����ھ�����������ã����Dz���������������������ȷ���ǣ�������
��ͼ��ʾ���ڹ⻬��Ե��ˮƽֱ���������������С��a��b��a������Ϊ2m��������Ϊ+q��b������Ϊm��������Ϊ+2q����������Զ�������˶���ijʱ��a��b����ٶȴ�С����Ϊv��1.5v�����ھ�����������ã����Dz���������������������ȷ���ǣ��������鿴�𰸺ͽ���>>
��Ŀ���������� ��Դ�� ���ͣ�
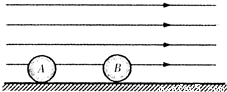
 ��2012?��ͷһģ����ͼ��ʾ���ڹ⻬��Եˮƽ���ϣ�������ľ�ԵС��P2��ֹ��O�㣮�������С��P1���ٶ�v0��A�����AB���������P2�����������������ٶ�Ϊ
��2012?��ͷһģ����ͼ��ʾ���ڹ⻬��Եˮƽ���ϣ�������ľ�ԵС��P2��ֹ��O�㣮�������С��P1���ٶ�v0��A�����AB���������P2�����������������ٶ�Ϊ| 2 |
| 3 |
| 4L0 |
| 3 |
| qE0 |
| m1 |
| 4v02 |
| 3L0 |
�鿴�𰸺ͽ���>>
��Ŀ���������� ��Դ�� ���ͣ�
 ��ͼ��ʾ���ڹ⻬��Ե��ˮƽ������һ����һ�����ȵ���Χ�ɵ��������߿�abcd����߳�ΪL���ܵ���ΪR�����ڴŸ�Ӧǿ��ΪB��������ֱ���µ���ǿ�ų�����ߣ�ͼ������MNΪ�ų�����߽磮�߿��ڴ�СΪF�ĺ��������������˶�������ab�߱�����MNƽ�У����߿����ٶ�v0����ų�����ʱ����ǡ���������˶������߿����ų��Ĺ����У�
��ͼ��ʾ���ڹ⻬��Ե��ˮƽ������һ����һ�����ȵ���Χ�ɵ��������߿�abcd����߳�ΪL���ܵ���ΪR�����ڴŸ�Ӧǿ��ΪB��������ֱ���µ���ǿ�ų�����ߣ�ͼ������MNΪ�ų�����߽磮�߿��ڴ�СΪF�ĺ��������������˶�������ab�߱�����MNƽ�У����߿����ٶ�v0����ų�����ʱ����ǡ���������˶������߿����ų��Ĺ����У��鿴�𰸺ͽ���>>
��Ŀ���������� ��Դ�� ���ͣ�
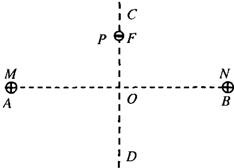 ��ͼ��ʾ���ڹ⻬��Եˮƽ���ϣ���������������ĵ���M��N���ֱ�̶���A��B���㣬OΪAB���ߵ��е㣬CDΪAB�Ĵ�ֱƽ���ߣ���CO֮���F���ɾ�ֹ�ͷ�һ���������С��P���費�ı�ԭ���ĵ糡�ֲ��������Ժ��һ��ʱ���ڣ�P��CD�������������˶�������������
��ͼ��ʾ���ڹ⻬��Եˮƽ���ϣ���������������ĵ���M��N���ֱ�̶���A��B���㣬OΪAB���ߵ��е㣬CDΪAB�Ĵ�ֱƽ���ߣ���CO֮���F���ɾ�ֹ�ͷ�һ���������С��P���費�ı�ԭ���ĵ糡�ֲ��������Ժ��һ��ʱ���ڣ�P��CD�������������˶�������������| A��С��P�Ĵ�����������С�����������˶�������������ϼ�С | B��С��P�Ĵ�����������С�����������˶�������ÿ�ξ���O��ʱ�����ʲ��ϼ�С | C������M��N�Ĵ�����ͬʱ�����ػ���������С��P�����˶����������ڲ��ϼ�С | D������M��N�Ĵ�����ͬʱ�����ػ���������С��P�����˶�������������ϼ�С |
�鿴�𰸺ͽ���>>
��Ŀ���������� ��Դ�� ���ͣ�
 ��ͼ��ʾ���ڹ⻬��Եˮƽ������ֱ������ϵxoy�����뾶ΪR=0.4m���ھ���С���ڱڹ⻬���ܱڼ�����Բ���ξ�Ե��ABˮƽ�̶��ڵڶ������ڣ�����A�˺�Բ��O�䶼��y���ϣ�B����x���ϣ�O��B��y�Ḻ����нǦ�=60�㣮������ϵ�ĵ�һ��������ͬ�����ڴ������ĸ���ֱ��ˮƽ�����ǿ�ų���a��b��cΪ�ų�������ֽ��ߣ����ǵ�ֱ�߷��̷ֱ�Ϊa��y=0.2��b��y=-0.1��c��y=-0.4����a��b��Χ��������b��c��Χ��������ڵĴŸ�Ӧǿ�ȷֱ�ΪB1��B2����һ�����������������ڴŸ�Ӧǿ�Ⱦ�ΪB0����һ����m=1.2��10-5kg�������q=1.0��10-6C��ֱ����С�ھ�Ե���ھ��Ĵ�����С���Ծ�Ե��A����v=2.0��10-2 m/s���ٶȴ�ֱy��������У����Ժ���˶������У�С���ܴ�ֱͨ��c��a���������Դ�ֱ��y����ٶȽ����Ե�ܶ����������˶�����
��ͼ��ʾ���ڹ⻬��Եˮƽ������ֱ������ϵxoy�����뾶ΪR=0.4m���ھ���С���ڱڹ⻬���ܱڼ�����Բ���ξ�Ե��ABˮƽ�̶��ڵڶ������ڣ�����A�˺�Բ��O�䶼��y���ϣ�B����x���ϣ�O��B��y�Ḻ����нǦ�=60�㣮������ϵ�ĵ�һ��������ͬ�����ڴ������ĸ���ֱ��ˮƽ�����ǿ�ų���a��b��cΪ�ų�������ֽ��ߣ����ǵ�ֱ�߷��̷ֱ�Ϊa��y=0.2��b��y=-0.1��c��y=-0.4����a��b��Χ��������b��c��Χ��������ڵĴŸ�Ӧǿ�ȷֱ�ΪB1��B2����һ�����������������ڴŸ�Ӧǿ�Ⱦ�ΪB0����һ����m=1.2��10-5kg�������q=1.0��10-6C��ֱ����С�ھ�Ե���ھ��Ĵ�����С���Ծ�Ե��A����v=2.0��10-2 m/s���ٶȴ�ֱy��������У����Ժ���˶������У�С���ܴ�ֱͨ��c��a���������Դ�ֱ��y����ٶȽ����Ե�ܶ����������˶������鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com