
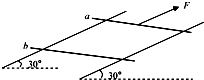
 ��ͼ��ʾ�������㹻����ƽ�н���������б���ã�������費�ƣ������Ϊ30�㣬������Ϊ0.5m����ǿ�ų���ֱ����ƽ�����£�B=0.2T������������ͬ�Ľ�����a��b�뵼�칹�ɱպϻ�·��a��b�������������ֱ�Ϊ3kg��2kg�����������ĵ����ΪR=1�����տ�ʼ������������ǡ�þ�ֹ���������Ħ�������Ƶ��ڻ���Ħ�������ֶ�a��ʩ��һƽ�е������ϵĺ���F=60N�������㹻����ʱ��������������ﵽ���ȶ�״̬����
��ͼ��ʾ�������㹻����ƽ�н���������б���ã�������費�ƣ������Ϊ30�㣬������Ϊ0.5m����ǿ�ų���ֱ����ƽ�����£�B=0.2T������������ͬ�Ľ�����a��b�뵼�칹�ɱպϻ�·��a��b�������������ֱ�Ϊ3kg��2kg�����������ĵ����ΪR=1�����տ�ʼ������������ǡ�þ�ֹ���������Ħ�������Ƶ��ڻ���Ħ�������ֶ�a��ʩ��һƽ�е������ϵĺ���F=60N�������㹻����ʱ��������������ﵽ���ȶ�״̬�������� ��1������a������ƽ����Ħ������
��2�����ݹ��ܹ�ϵ��ϵ��������ĵ��ȣ���ƽ�������������
��3����a����b���ֱ�����ţ�ٵڶ�������ʽ������������������ﵽ�ȶ�״̬ʱ��b�����ܵİ�������
��� �⣺��1��a��ǡ�þ�ֹ����ƽ�⣬����ƽ�������У�
${m_a}gsin{30^0}=��{m_a}gcos{30^0}$
��ã�$��=\frac{{\sqrt{3}}}{3}$��
��2���˹��̶�a��b��һ����ݹ��ܹ�ϵ�ɵã�
$\left.\begin{array}{l}{Q=F{x}_{a}-��{m}_{a}gsin3{0}^{0}+��{m}_{a}gcos3{0}^{0}��{x}_{a}-��{m}_{b}gsin3{0}^{0}+��{m}_{b}gcos3{0}^{0}��{x}_{b}}\end{array}\right.$$\left.\begin{array}{l}{-\frac{1}{2}{m}_{a}{v}_{a}^{2}-\frac{1}{2}{m}_{b}{v}_{b}^{2}}\end{array}\right.$
��ã�Q=85J
���ݵ�����ļ��㹫ʽ�ɵã�$q=\overline I•��t$
���ݱպϵ�·��ŷķ���ɿɵã�$\overline I=\frac{\overline E}{2R}$
���ݷ����ڵ�Ÿ�Ӧ���ɿɵã�$\overline E=\frac{����}{��t}=\frac{B•��S}{��t}$
��$q=\frac{{B•d•��{x_a}-{x_b}��}}{2R}=0.15C$��
��3�������ȶ�ʱ����ͬ�ļ��ٶ������ȼ���ֱ�ߣ���ʱ�����к㶨���ٶȲ
��a������ţ�ٵڶ����ɿɵã�$F-{m_a}gsin{30^0}-��{m_a}gcos{30^0}-{F_��}={m_a}•a$��
��b������ţ�ٵڶ����ɿɵã�${F_��}-{m_b}gsin{30^0}-��{m_b}gcos{30^0}={m_b}•a$
������ã�F��=24N��
�𣺣�1���������뵼���Ķ�Ħ������Ϊ$\frac{\sqrt{3}}{3}$��
��2���˹����л�·�в����ĵ���Ϊ85J��ͨ��a�������ĵ����Ϊ0.15C��
��3���������������ﵽ�ȶ�״̬ʱ��b�����ܵİ�����Ϊ24N��
���� �������������о�����һҪ��ȷ����ab������������о����������Ĵ�С����Ҫ��ȷ����������ת����������õ�����ʽ�������������������������Ӧ�ô��˶����̺��������������о���������ѧ���ɷ����ͽ�����⣮


 ��������һ���þ�ϵ�д�
��������һ���þ�ϵ�д� Сѧ��10����Ӧ����ϵ�д�
Сѧ��10����Ӧ����ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ���������� ��Դ�� ���ͣ���ѡ��
 ��ͼ��ʾ��xOyƽ��λ�ڹ⻬ˮƽ�����ϣ���O��x��2L�������ڴ�������ǿ�ų����ų�����ֱ��xOyƽ�����£���ͬ�ֲ����ƳɵĴ�ϸ���ȵ��������ε��߿��ڸ�ˮƽ�����ϣ�AB��DE�߾���ǡΪ2L����ʩ��һˮƽ���ҵ�����F�����߿�ˮƽ���������˶���DE����y��ʼ��ƽ�У����߿�DE�߸ս���ų���ʼ��ʱ�����߿��еĸ�Ӧ����i��ȡ��ʱ�뷽��ĵ���Ϊ������ʱ��t�ĺ���ͼ�������F��ʱ��t�ĺ���ͼ������ǣ�������
��ͼ��ʾ��xOyƽ��λ�ڹ⻬ˮƽ�����ϣ���O��x��2L�������ڴ�������ǿ�ų����ų�����ֱ��xOyƽ�����£���ͬ�ֲ����ƳɵĴ�ϸ���ȵ��������ε��߿��ڸ�ˮƽ�����ϣ�AB��DE�߾���ǡΪ2L����ʩ��һˮƽ���ҵ�����F�����߿�ˮƽ���������˶���DE����y��ʼ��ƽ�У����߿�DE�߸ս���ų���ʼ��ʱ�����߿��еĸ�Ӧ����i��ȡ��ʱ�뷽��ĵ���Ϊ������ʱ��t�ĺ���ͼ�������F��ʱ��t�ĺ���ͼ������ǣ�������| A�� |  | B�� | 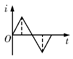 | C�� |  | D�� | 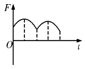 |
�鿴�𰸺ͽ���>>
��Ŀ���������� ��Դ�� ���ͣ�ѡ����
| A�� | �ڹ��ЧӦʵ���У���ֹ��ѹ�������Ƶ���� | |
| B�� | �Ƚ����ԽС����ʾԭ�Ӻ��к��ӽ�ϵ�Խ�ι̣�ԭ�Ӻ�Խ�ȶ� | |
| C�� | һ����ԭ�Ӵ�n=3�����巢��ԾǨ������ֻ����һ��Ƶ�ʵĹ��� | |
| D�� | ������ǿ����õ�һ�ֱ��֣�ԭ�Ӻ˳߶��ڣ������ȿ�����С |
�鿴�𰸺ͽ���>>
��Ŀ���������� ��Դ�� ���ͣ���ѡ��
| A�� | ľ�����ӵ���������Ϊ15��1 | |
| B�� | ���ڶ���ͬ�����ӵ�����ͬ���ٶ��ٴ�����ľ���δ����������ľ����3m/s���ٶ������˶� | |
| C�� | �������ľ��ֹͣ�˶���Ӧ����ͬ���ٶ�����ľ��ӭ������4��ͬ���ӵ����ӵ���δ������ | |
| D�� | �������ľ��ֹͣ�˶���Ӧ����ͬ���ٶ�����ľ��ӭ������8��ͬ���ӵ����ӵ���δ������ |
�鿴�𰸺ͽ���>>
��Ŀ���������� ��Դ�� ���ͣ�ѡ����
| A�� | ������������������������ | B�� | �������������������ܼ��� | ||
| C�� | �������������������ܼ��� | D�� | ������������������������ |
�鿴�𰸺ͽ���>>
��Ŀ���������� ��Դ�� ���ͣ���ѡ��
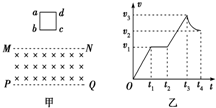 ��ͼ����ʾ��λ����ֱƽ���ڵ������αպϽ����߿�abcd������Ϊm������ΪR�����·���һ����ֱ���߿�ƽ���������ǿ�ų�����MN��PQ��ˮƽ�߽磬�����߿��bc��ƽ�У����ý����߿��ɾ�ֹ��ʼ���䣬ͼ���ǿ�ʼ���䵽��ȫ�����ų�����˲���v-tͼ���������ٶ�Ϊg�����ƿ���������������
��ͼ����ʾ��λ����ֱƽ���ڵ������αպϽ����߿�abcd������Ϊm������ΪR�����·���һ����ֱ���߿�ƽ���������ǿ�ų�����MN��PQ��ˮƽ�߽磬�����߿��bc��ƽ�У����ý����߿��ɾ�ֹ��ʼ���䣬ͼ���ǿ�ʼ���䵽��ȫ�����ų�����˲���v-tͼ���������ٶ�Ϊg�����ƿ���������������| A�� | �ս���ų�ʱ��Ӧ����������adcba���� | |
| B�� | t4-t3=t2-t1 | |
| C�� | �ų��ĴŸ�Ӧǿ��Ϊ$\frac{1}{v1��t2-t1��}$$\sqrt{\frac{mgR}{{v}_{1}}}$ | |
| D�� | �����߿���0��t4��ʱ����������������Ϊ2mgv1��t2-t1��+$\frac{1}{2}$m��v32-v22�� |
�鿴�𰸺ͽ���>>
��Ŀ���������� ��Դ�� ���ͣ�ѡ����
| A�� | $\sqrt{\frac{4{v}^{2}-{{v}_{0}}^{2}}{{v}^{2}-{{v}_{0}}^{2}}}$t | B�� | $\sqrt{\frac{4{v}^{2}-{{v}_{0}}^{2}}{3{v}^{2}-{{v}_{0}}^{2}}}$t | ||
| C�� | $\sqrt{\frac{3{v}^{2}}{4{g}^{2}}+{t}^{2}}$ | D�� | 2t |
�鿴�𰸺ͽ���>>
��Ŀ���������� ��Դ�� ���ͣ�������
 ��ͼ��ʾ������Ϊ4m���㹻��ľ��C��ֹ�ڹ⻬ˮƽ���ϣ�������Ϊm������С����A��B����C����ˣ�A��B�����Ϊd����ͬʱ��A��Bʩ��ˮƽ���ҵ�˲ʱ������ʹ֮�ֱ��ó��ٶ�v0��3v0��A��Bʼ��δ����C����A��B��C֮��Ķ�Ħ�������ֱ�Ϊ�̺�3�̣���
��ͼ��ʾ������Ϊ4m���㹻��ľ��C��ֹ�ڹ⻬ˮƽ���ϣ�������Ϊm������С����A��B����C����ˣ�A��B�����Ϊd����ͬʱ��A��Bʩ��ˮƽ���ҵ�˲ʱ������ʹ֮�ֱ��ó��ٶ�v0��3v0��A��Bʼ��δ����C����A��B��C֮��Ķ�Ħ�������ֱ�Ϊ�̺�3�̣����鿴�𰸺ͽ���>>
��Ŀ���������� ��Դ�� ���ͣ�ѡ����
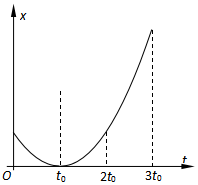 ij�ʵ���ͬһֱ�����˶�ʱ��λ��-ʱ�䣨x-t��ͼ��Ϊһ�����ߣ����������߹���t=t0�Գƣ��㣨t0��0��Ϊ�����ߵĶ��㣮����˵����ȷ���ǣ�������
ij�ʵ���ͬһֱ�����˶�ʱ��λ��-ʱ�䣨x-t��ͼ��Ϊһ�����ߣ����������߹���t=t0�Գƣ��㣨t0��0��Ϊ�����ߵĶ��㣮����˵����ȷ���ǣ�������| A�� | ���ʵ���0-3t0��ʱ�����˶����ֲ��� | |
| B�� | ��t0ʱ�̣��ʵ�ļ��ٶ�Ϊ�� | |
| C�� | ��0-3t0��ʱ���ڣ��ٶ��ȼ�С������ | |
| D�� | �ʵ���0-t0��t0-2t0��2t0-3t0�������ʱ�����ͨ����λ�ƴ�С֮��Ϊ1��1��4 |
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com