 

(1) ,T为电磁打点计时器打点的时间间隔,r为圆盘的半径,x2、x1是纸带上选定的两点分别对应的米尺的刻度值,n为选定的两点间的打点数(含两点)。 ,T为电磁打点计时器打点的时间间隔,r为圆盘的半径,x2、x1是纸带上选定的两点分别对应的米尺的刻度值,n为选定的两点间的打点数(含两点)。 (2)6.8/s。 难度:      题型: 知识点: 题型: 知识点:
一个实验小组在“探究弹力和弹簧伸长的关系”的实验中,使用两根不同的轻质弹簧a和b,得到弹力与弹簧长度的图象如图所示。下列表述正确的是 ( ) A.a的原长比b的长 B.a的劲度系数比b的大 C.a的劲度系数比b的小 D.测得的弹力与弹簧的长度成正比 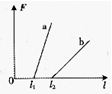
B 难度:      题型: 知识点: 题型: 知识点:
在“验证力的平行四边形定则”实验中,需要将橡皮条的一端固定在水平木板上,另一端系上两根细绳,细绳的另一端都有绳套(如图)。实验中需用两个弹簧秤分别勾住绳套,并互成角度地拉橡皮条。某同学认为在此过程中必须注意以下几项: A. 两根细绳必须等长。 B.橡皮条应与两绳夹角的平分线在同一直线上。 C. 在使用弹簧秤时要注意使弹簧秤与木板平面平行。 其中正确的是 。(填入相应的字母) 
C 难度:      题型: 知识点: 题型: 知识点:
在做“验证机械能守恒定律”实验时,用打点计时器打出纸带如图所示,其中A点为打下的第一个点,0、1、2……为连续的相邻计数点。现测得两相邻计数点之间的距离分别为s1、s2、s3、s4、s5、s6,已知计数点间的时间间隔为T。根据纸带测量出的数据可以求出此实验过程中重锤下落运动的加速度大小的表达式为 ,打下第5号计数点时,纸带运动的瞬时速度大小的表达式为 。要验证机械能守恒定律,为减小实验误差,应选择打下第 号和第 号计数点之间的过程为研究对象。
 或 或 ……;(s5+s6)/2T;1,5 ……;(s5+s6)/2T;1,5
难度:      题型: 知识点: 题型: 知识点:
如图4所示为某同学用多用电表欧姆档测量一个电阻阻值的示数和档位情况,则这个电阻的阻值约为 Ω。如果想测量的更精确些,应怎样调节多用电表后再进行测量?答: 。 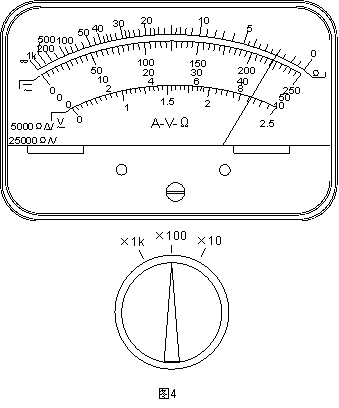
答案:2.0×102,换用×10Ω档并调零 难度:      题型: 知识点: 题型: 知识点:
下图为一正在测量中的多用电表表盘。 (1)如果是用直流10V档测量电压,则读数为 V。(2)如果是用×100Ω档测量电阻,则读数为 Ω。(3)如果是用直流5mA档测量电流,则读数为 mA。 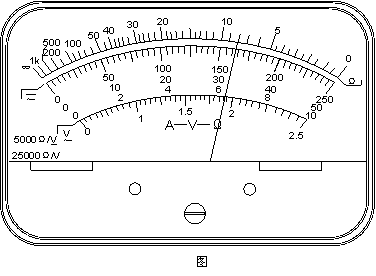
6.5;8.0×102;3.25 难度:      题型: 知识点: 题型: 知识点:
已知太阳到地球与地球到月球的距离的比值约为390,月球绕地球旋转的周期约为27天。利用上述数据以及日常的天文知识,可估算出太阳对月球与地球对月球的万有引力的比值约为( ) A.0.2 B.2 C.20 D.200 B 难度:      题型: 知识点: 题型: 知识点:
土星周围有美丽壮观的“光环”,组成环的颗粒是大小不等、线度从1μm到10m的岩石、尘埃,类似于卫星,它们与土星中心的距离从7.3×104km延伸到1.4×105km。已知环的外缘颗粒绕土星做圆周运动的周期约为14h,引力常量为6.67×10-11N?m2/kg2,则土星的质量约为(估算时不考虑环中颗粒间的相互作用) ( ) A.9.0×1016kg B.6.4×1017kg C.9.0×1025kg D.6.4×1026kg D 难度:      题型: 知识点: 题型: 知识点:
在中子衍射技术中,常利用热中子研究晶体的结构,因为热中子的德布罗意波长与晶体中原子间距相近。已知中子质量m=1.67×10-27kg,普朗克常量h=6.63×10-34J·s,可以估算德布罗意波长λ=1.82×10-10m的热中子动能的数量级为 ( ) (A)10-17J (B)10-19J (C)10-21J (D)10-24 J C 难度:      题型: 知识点: 题型: 知识点:
人眼对绿光最为敏感。正常人的眼睛接收到波长为530nm的绿光时,只要每秒有6个绿光的光子射入瞳孔,眼睛就能察觉。普朗克常量为6.63×10-34J×s,光速为3.0×108m/s,则人眼能察觉到绿光时所接收到的最小功率是 A. 2.3×10-18W B. 3.8×10-19W C. 7.0×10-48W D.1.2×10-48W A 难度:      题型: 知识点: 题型: 知识点:
在如图所示的四个图象中,能够正确反映一种元素的同位素原子核的质量数M与其中子数N之间的关系的是 ( ) 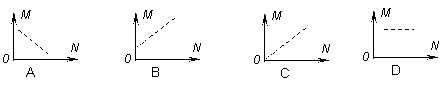 
B 难度:      题型: 知识点: 题型: 知识点:
一个小孩在蹦床上作游戏,他从高处落到蹦床上后又被弹起到原高度。小孩从高处开始下落到弹回的整个过程中,他的运动速度随时间变化的图象如图所示,图中oa段和cd段为直线。则根据此图象可知,小孩和蹦床相接触的时间为 ( ) A.t2 ~ t4 B.t1 ~ t4 C.t1 ~ t5 D.t2 ~ t5 
C 难度:      题型: 知识点: 题型: 知识点:
一根质量为M的直木棒,悬挂在O点,有一只质量为m的猴子抓着木棒,如图甲所示。剪断悬挂木棒的细绳,木棒开始下落,同时猴子开始沿棒向上爬,设在一段时间内木棒沿竖直方向下落,猴子对地的高度保持不变。忽略空气阻力。则图乙的四个图象中能正确反映在这段时间内猴子对木棒作功的功率随时间变化的关系的是: ( )
B 难度:      题型: 知识点: 题型: 知识点:
如图所示,是一个说明示波管工作原理的示意图,电子经电压U1加速后以速度v0垂直进入偏转电场,离开电场时的偏转量是h,两平行板间距离为d,电势差是U2,板长是l,每单位电压引起的偏转量(h/U)叫做示波管的灵敏度,那么要提高示波管的灵敏度,可以采取下列哪些方法 ( ) A.增大两板间电势差U2 B.尽可能使板长l短一些 C.尽可能使板距d小一些 D.使加速电压U1升高一些 
C 难度:      题型: 知识点: 题型: 知识点:
如图甲为电视机显像管的整体结构示意图,其左端尾部是电子枪,被灯丝K加热的阴极能发射大量的“热电子”,“热电子”经过加速电压U加速后形成电子束,高速向右射出。在显像管的颈部装有两组相互垂直的磁偏转线圈L,图乙是其中一组“纵向”偏转线圈从右侧向左看去的示意图,当在磁偏转线圈中通入图示方向的电流时,在显像管颈部形成水平向左(即甲图中垂直纸面向外)的磁场,使自里向外(即甲图中自左向右)射出的电子束向上偏转;若该线圈通入相反方向的电流,电子束则向下偏转。改变线圈中电流的大小,可调节偏转线圈磁场的强弱,电子束的纵向偏转量也随之改变。这样,通过控制加在“纵向”偏转线圈上的交变电压,就可以控制电子束进行“纵向”(竖直方向)扫描。同理,与它垂直放置在颈部的另一组“横向”偏转线圈,通入适当的交变电流时,能控制电子束进行“横向”(水平方向)扫描。 两组磁偏转线圈同时通入适当的交变电流时,可控制电子束反复地在荧光屏上自上而下、自左而右的逐行扫描,从而恰好能将整个荧光屏“打亮”。如果发现荧光屏上亮的区域比正常时偏小,则可能是下列哪些原因引起的 ( ) A.阴极发射电子的能力不足,单位时间内发射的电子数偏少 B.偏转线圈在显像管的位置过于偏右 C.加速电场电压过低,使得电子速率偏小 D.通过偏转线圈的交变电流的最大值偏小,使得偏转磁场的最大磁感强度偏小  
D 难度:      题型: 知识点: 题型: 知识点:
在无线电仪器中,常需要在距离较近处安装两个线圈,并要求当一个线圈中有电流变化时,对另一个线圈中的电流的影响尽量小。则图中两个线圈的相对安装位置最符合该要求的是 ( )
D 难度:      题型: 知识点: 题型: 知识点:
如图所示是进行训练用的“跑步机”示意图,质量为m运动员踩在与水平面成α角的传送皮带上,传送皮带运动过程中受到的阻力恒为f。当运动员用力蹬传送皮带,使其以速度v匀速向后运动,则在这一过程中,下列说法中正确的是 ( ) A.人脚对传送皮带的摩擦力是传送皮带所受的阻力 B.人对传送皮带不做功 C.人对传送皮带做功的功率为mgv D.人对传送皮带做功的功率为fv
D 难度:      题型: 知识点: 题型: 知识点:
如图所示,A、B两质点以相同的水平速度v0沿x轴正方向抛出,A在竖直平面内运动,落地点为P1,B沿光滑斜面运动,落地点为P2。P1和P2在同一水平面上,不计空气阻力。则下面说法中正确的是 ( ) A.A、B的运动时间相同 B.A、B沿x轴方向的位移相同 C.A、B落地时的动量相同 D.A、B落地时的动能相同 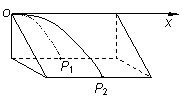 
D 难度:      题型: 知识点: 题型: 知识点:
如图所示,一个小球从斜面上被抛出,抛出时初速度v0的方向与斜面垂直,它最后落到斜面上的某点。不计空气阻力,下面关于小球在空中的运动的说法中正确的是( ) A.小球的运动可以看作是沿水平方向的匀速运动和竖直向下的自由落体运动的叠加 B.小球的运动可以看作是沿垂直斜面方向的匀速运动和平行斜面向下的自由落体运动的叠加 C.小球的运动可以看作是沿垂直斜面方向的匀速运动和沿斜面向下的匀加速运动的叠加 D.小球的运动可以看作是沿水平方向的匀速运动和沿竖直方向的匀变速运动的叠加 
D 难度:      题型: 知识点: 题型: 知识点:
在一根软铁棒上绕有一组线圈,a、c是线圈的两端,b为中心抽头。把a端和b抽头分别接到两条平行金属导轨上,导轨间有匀强磁场,方向垂直于导轨所在平面并指向纸内,如图所示。金属棒PQ在外力作用下以图示位置为平衡位置左右作简谐运动,运动过程中保持与导轨垂直,且两端与导轨始终接触良好。下面的哪些过程中a、c点的电势都比b点的电势高? ( ) A.PQ从平衡位置向左边运动的过程中 B.PQ从左边向平衡位置运动的过程中 C.PQ从平衡位置向右边运动的过程中 D.PQ从右边向平衡位置运动的过程中 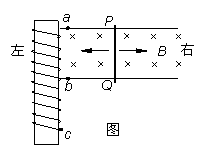
C 1 2 3 4 ...52 53 54 下一页 ? | 
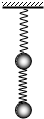 s1和s2表示劲度系数分别为k1和k2的两弹簧,k1>k2;a、b表示质量分别为ma和mb的两个小物体,ma>mb,将弹簧与物体如图所示方式悬挂起来,若要求两弹簧的总长度最大,则应使( )
s1和s2表示劲度系数分别为k1和k2的两弹簧,k1>k2;a、b表示质量分别为ma和mb的两个小物体,ma>mb,将弹簧与物体如图所示方式悬挂起来,若要求两弹簧的总长度最大,则应使( )

 名校课堂系列答案
名校课堂系列答案 分享到
分享到