
 ���ٴ��ǽ���·���ϳ�����һ�ֽ�ͨ��ʩ����ijС���ſ���һ���ٴ�����ͼ������һ����Ѳ�߳���������ٶ�25m/s��С���ſھ�����������ٴ�90mʱ���췢��һ�ӷ�����10m/s���ٶ���綯������ͨ�����ٴ����綯��ʼ�����٣�����Ѳ�߳�Ҫ�ȼ��ٵ�5m/sͨ�����ٴ������ٴ��Ŀ��Ⱥ��Բ��ƣ������ٵ�5m/s��������2.5m/s2�ļ��ٶȼ��ٵ�����ٶȼ����ϣ��������������У�Ѳ�߳����ӷ�����ˮƽֱ�����˶�����Ӿ��췢���ӷ������ӷ���Ҫ��ʱ�䣮
���ٴ��ǽ���·���ϳ�����һ�ֽ�ͨ��ʩ����ijС���ſ���һ���ٴ�����ͼ������һ����Ѳ�߳���������ٶ�25m/s��С���ſھ�����������ٴ�90mʱ���췢��һ�ӷ�����10m/s���ٶ���綯������ͨ�����ٴ����綯��ʼ�����٣�����Ѳ�߳�Ҫ�ȼ��ٵ�5m/sͨ�����ٴ������ٴ��Ŀ��Ⱥ��Բ��ƣ������ٵ�5m/s��������2.5m/s2�ļ��ٶȼ��ٵ�����ٶȼ����ϣ��������������У�Ѳ�߳����ӷ�����ˮƽֱ�����˶�����Ӿ��췢���ӷ������ӷ���Ҫ��ʱ�䣮 ���� ���������ȼ���ֱ���˶���Ȼ�����ȼ���ֱ���˶�����������ֱ���˶����ӷ�һֱ������ֱ���˶��������λ�����ӷ�λ��֮��Ϊ50mʱ�������ӷ���Ӧ���ȱ���ֱ���˶������������˶���������������ӷ���ʱ�䣮
��� �⣺�辯����ٶ�Ϊv1=25m/s��������ٴ�ʱ�ٶ�Ϊ��v2=5m/s����ʼʱ���������ٴ�����Ϊx0=90m���쵽����ٴ�ʱ��Ϊ��${t_1}=\frac{x_0}{\bar v}=\frac{x_0}{{\frac{{{v_1}+{v_2}}}{2}}}=6s$
�����ʱ�����ӷ�ǰ���ľ���Ϊx1=vt1=60m
���쵽����ٴ�֮�����Լ��ٶ�a=2.5m/s2����ǰ�����������ٴδﵽ����ٶ�v1=25m/sʱ������ʱ��Ϊt2�������ٶȹ�ʽ��
v1=v2+at2��
�����������t2=8s��
����8s�ڣ�����ǰ���ľ���Ϊ${x_2}={v_2}{t_2}+\frac{1}{2}at_2^2=120m$
���ͬʱ���ӷ�ǰ���ľ���Ϊx3=vt2=80m
�˺�������ٶ�v1=25m/sǰ�����辭��t3ʱ�侯�����ӷ�����v1t3=��x1+x2-x3��+v��t3
�����õ�t3=4/3s��
���Ӿ��췢���ӷ������ӷ�������Ҫ��ʱ��Ϊ$t={t_1}+{t_2}+{t_3}=\frac{46}{3}s��15.33s$
�𣺴Ӿ��췢���ӷ������ӷ���Ҫ��ʱ��15.33s��
���� ���⿼���������⣬��������������ӷ����˶����̣�Ӧ���ȱ���ֱ���˶����ɡ������˶����ɼ�����ȷ���⣻��������˶����̣��ҳ����������ǽ���Ĺؼ���


 ���ɿ��õ�Ԫ������ĩר����100��ϵ�д�
���ɿ��õ�Ԫ������ĩר����100��ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ���������� ��Դ�� ���ͣ�ѡ����
| A�� | 35 km/h | B�� | 55 km/h | C�� | 45 km/h | D�� | 50 km/h |
�鿴�𰸺ͽ���>>
��Ŀ���������� ��Դ�� ���ͣ������
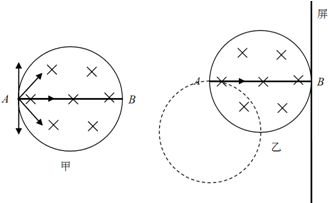
�鿴�𰸺ͽ���>>
��Ŀ���������� ��Դ�� ���ͣ���ѡ��
| A�� | �ٶȸı����Ĵ�Сһ����10m/s | |
| B�� | �ٶȸı����Ĵ�С������6m/s | |
| C�� | �ٶȸı����ķ���һ������ٶȷ�����ͬ | |
| D�� | �ٶȸı����ķ����������ٶȷ����෴ |
�鿴�𰸺ͽ���>>
��Ŀ���������� ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ���������� ��Դ�� ���ͣ�ѡ����
| A�� | �����ˮƽ�����ѹ���������� | |
| B�� | �����ķ������ָ����� | |
| C�� | �˵ĵ���һ���ظ˷��� | |
| D�� | ����������ѹ�������淢���α������ |
�鿴�𰸺ͽ���>>
��Ŀ���������� ��Դ�� ���ͣ�ѡ����
| A�� | $\frac{{x}_{1}}{{x}_{2}}$=$\frac{{t}_{1}}{{t}_{2}}$ | B�� | v=$\frac{2��{x}_{1}+{x}_{2}��}{{t}_{1}+{t}_{2}}$ | ||
| C�� | $\frac{{x}_{1}}{{t}_{1}}$=$\frac{{x}_{2}}{{t}_{2}}$=$\frac{{x}_{1}+{x}_{2}}{{t}_{1}+{t}_{2}}$ | D�� | $\frac{{a}_{1}}{{a}_{2}}$=$\frac{{t}_{1}}{{t}_{2}}$ |
�鿴�𰸺ͽ���>>
��Ŀ���������� ��Դ�� ���ͣ���ѡ��
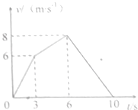 ��������ֱ�����˶���v-tͼ����ͼ��ʾ��ȡ��ֱ����Ϊ��������ͼ����Կ������壨������
��������ֱ�����˶���v-tͼ����ͼ��ʾ��ȡ��ֱ����Ϊ��������ͼ����Կ������壨������| A�� | 0��10s��һֱ�����˶� | B�� | 3��6s�ڼ��ٶ���� | ||
| C�� | 0��3s�������˶���6��10s�������˶� | D�� | 0��3s��6��10s�ڼ��ٶȷ��� |
�鿴�𰸺ͽ���>>
��Ŀ���������� ��Դ�� ���ͣ������
 Ϊ̽����������һ��ʱ�������˶��ļ��ٶ��������Ĺ�ϵ����ijͬѧ�������ͼ��ʾ��ʵ��װ�ã�A1A2����ǿ��Ե��ڵij�б�棬B�Dz���Ħ������С�������м�ʱ�����׳ߡ���ƽ������ȣ�������в����е���գ����ò�õ����������ű�ʾ��
Ϊ̽����������һ��ʱ�������˶��ļ��ٶ��������Ĺ�ϵ����ijͬѧ�������ͼ��ʾ��ʵ��װ�ã�A1A2����ǿ��Ե��ڵij�б�棬B�Dz���Ħ������С�������м�ʱ�����׳ߡ���ƽ������ȣ�������в����е���գ����ò�õ����������ű�ʾ���鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com