
 ij��Ϸװ�÷�����ֱƽ���ڣ���ͼ��ʾ��װ���ɴֲ��������ι��AB�⻬��Բ�����BCD���ɣ����Ƶ������ɽ����ڹ���ϵ�С���Բ�ͬ��ˮƽ���ٶ���A�����룬���С����Բ�������ߵ�Dˮƽ�׳������뿨���е÷֣�Բ���뾶ΪR��O��ΪԲ����Բ�ģ�CΪԲ�������͵㣬�����߹����A�����������ԭ��O�ϣ������Բ��������B�㣬�����߹������Ϊy=ax2��0��a��$\frac{1}{4R}$������BO��C=�ȣ�x��ǡ�ý��뾶O��D�ֳ���ȵ����룬����ΪP��x����Բ������Q�㣬��
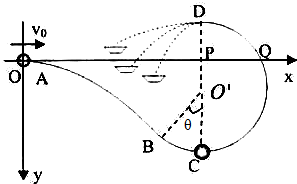
ij��Ϸװ�÷�����ֱƽ���ڣ���ͼ��ʾ��װ���ɴֲ��������ι��AB�⻬��Բ�����BCD���ɣ����Ƶ������ɽ����ڹ���ϵ�С���Բ�ͬ��ˮƽ���ٶ���A�����룬���С����Բ�������ߵ�Dˮƽ�׳������뿨���е÷֣�Բ���뾶ΪR��O��ΪԲ����Բ�ģ�CΪԲ�������͵㣬�����߹����A�����������ԭ��O�ϣ������Բ��������B�㣬�����߹������Ϊy=ax2��0��a��$\frac{1}{4R}$������BO��C=�ȣ�x��ǡ�ý��뾶O��D�ֳ���ȵ����룬����ΪP��x����Բ������Q�㣬������ ��1��BCD�ǹ⻬�Ĺ���ʴ�B��Q�Ĺ�����ֻ���������������ݶ��ܶ������С����B����ٶȼ��ɣ�
��2����A��B�Ĺ�����ֻ������������������Ϊ�����DZ�������������������Ĺ����������С����A��ij��ٶȣ�
��3��Ҫ��С���е����ʧ��С�����������֪����С���A����ƽ���˶������������غ�ʱ��С����ʧ�Ļ�е����С����ƽ���˶��������С����B��ʱ�ٶȣ����ɶ��ܶ�����С������ߵ���͵�ʱ��ֱ����ĺ������ṩС��Բ���˶�������������⼴�ɣ�
��� �⣺��1��С���B��Q�Ĺ������ڹ⻬��Բ��������˶���ȫ������ֻ���������������ݶ��ܶ����У�
-mg��Rcos��+$\frac{R}{2}$��=0-$\frac{1}{2}m{v}_{B}^{2}$
���С����B��ʱ���ٶȣ�vB=$\sqrt{gR��1+2cos�ȣ�}$
��2�������������Ϊ�����߹���ֲڣ�С���ڹ�����˶�ʱ����Ħ�����DZ������ʲ������Ħ������С�����Ĺ����������ɶ��ܶ������С����A��ʱ���ٶȣ�
��3���������֪��ҪʹС����ʧ�Ļ�е����С����С���������˶���������Ħ�������������Ե�С����ƽ���˶����ǡ���������߹���غ�ʱ��С���˶���������Ħ���������������У�
����ƽ���˶������У�
x=v0t
y=$\frac{1}{2}g{t}^{2}$
�ɵ� y=$\frac{g}{2{v}_{0}}{x}^{2}$=ax2
���ԣ�v0=$\sqrt{\frac{g}{2a}}$
С���A��C��ֻ�����������У�
mg��R+$\frac{R}{2}$��=$\frac{1}{2}m{v}_{C}^{2}$-$\frac{1}{2}m{v}_{0}^{2}$
С������͵���ֱ����ĺ����ṩԲ���˶����������У�
FNC-mg=m$\frac{{v}_{C}^{2}}{R}$
������ʽ�ɽ�ã�FNC=4mg+$\frac{mg}{2aR}$
��A��D������ֻ�����������У�
-mg$\frac{R}{2}$=$\frac{1}{2}m{v}_{D}^{2}$-$\frac{1}{2}m{v}_{0}^{2}$
��ã�vD=$\sqrt{\frac{g}{2a}-gR}$
��Ϊ0��a��$\frac{1}{4R}$�������ԣ�vD��$\sqrt{gR}$
����D����FND+mg=m$\frac{{v}_{D}^{2}}{R}$
�ɵã�FND=$\frac{mg}{2aR}$-2mg
���Կɵã�$\frac{{F}_{ND}}{{F}_{NC}}$=$\frac{1-4aR}{1+8aR}$
��
��1����С����ijһ���ٶ�ˮƽ��A����������С���ع���˶�����A�ȸߴ�Q���ٶȼ�Ϊ0��С���˶���B����ٶ�Ϊ$\sqrt{gR��1+2cos�ȣ�}$��
��2���ɣ�1���õ���B����ٶȣ��������С����A��������ٶȣ���Ϊ�������AD��Ħ����������������Ĺ���
��3��С������ߵ�D�Թ��������������͵�C�Թ�����������ı�ֵΪ$\frac{1-4aR}{1+8aR}$��
���� �������ڶ��ܶ�����Բ���˶�����͵��ۺ��⣬�ܸ�������Ҫ���������߶λ�е����ʧ��С�жϳ�С����ƽ���˶��Ĺ켣���������غ�ʱ��Ħ�������������ǽ�������ʵ�һ���ؼ��㣮


 ��У����ϵ�д�
��У����ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ���������� ��Դ�� ���ͣ�ѡ����
| A�� | ��ֹ�����岻�����ܻ���Ħ���� | |
| B�� | ͬһ�����ڵ����������������С��ȣ�������ͬ | |
| C�� | �����Ĵ�С��Ȼ��������һ������ | |
| D�� | �����ϵ�����ܵ���֧���������������α������ |
�鿴�𰸺ͽ���>>
��Ŀ���������� ��Դ�� ���ͣ���ѡ��

| A�� | �� | B�� | �� | C�� | �� | D�� | �� |
�鿴�𰸺ͽ���>>
��Ŀ���������� ��Դ�� ���ͣ���ѡ��
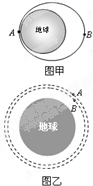 �ҹ����ռ�ʵ���ҡ��칬һ�š�������Ϊһ��Բ����ͼ����ʾ�����������λ�ڸ���Բ��һ�������ϣ�A��B����ֱ����������й���ϵĽ��ص��Զ�ص㣮��A���ڵ��渽���������������������Ժ��Բ��ƣ�֮���칬һ�š��͡����۰˺š��Խӣ�����ͼ��ʾ��A�������칬һ�š���B���������۰˺š�������Ϊ���ԵĹ������������Ϣ�������ж���������
�ҹ����ռ�ʵ���ҡ��칬һ�š�������Ϊһ��Բ����ͼ����ʾ�����������λ�ڸ���Բ��һ�������ϣ�A��B����ֱ����������й���ϵĽ��ص��Զ�ص㣮��A���ڵ��渽���������������������Ժ��Բ��ƣ�֮���칬һ�š��͡����۰˺š��Խӣ�����ͼ��ʾ��A�������칬һ�š���B���������۰˺š�������Ϊ���ԵĹ������������Ϣ�������ж���������| A�� | ͼ���������˶���A��ʱ������һ������7.9km/s | |
| B�� | ͼ������Ҫ������B�����ڵĸ߶�������Բ���˶�������B����� | |
| C�� | ͼ���С��칬һ�š������ļ��ٶȴ��ڡ����۰˺š������ļ��ٶ� | |
| D�� | ͼ���С����۰˺š������п����롰�칬һ�š�ʵ�ֶԽ� |
�鿴�𰸺ͽ���>>
��Ŀ���������� ��Դ�� ���ͣ���ѡ��
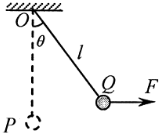 ��ͼ��ʾ��һ����Ϊm��С���ó�Ϊl������������O�㣬��ʼʱ��С��ֹ��P�㣮��һ��С����ˮƽ����F�����£���P�㻺�����ƶ���Q�㣬��ʱ��������ֱ����н�Ϊ�ȣ��ڶ�����ˮƽ����F�������£���P�㿪ʼ�˶���ǡ���ܵ���Q�㣬���ƿ����������������ٶ�Ϊg���������������̣�����˵������ȷ���ǣ�������
��ͼ��ʾ��һ����Ϊm��С���ó�Ϊl������������O�㣬��ʼʱ��С��ֹ��P�㣮��һ��С����ˮƽ����F�����£���P�㻺�����ƶ���Q�㣬��ʱ��������ֱ����н�Ϊ�ȣ��ڶ�����ˮƽ����F�������£���P�㿪ʼ�˶���ǡ���ܵ���Q�㣬���ƿ����������������ٶ�Ϊg���������������̣�����˵������ȷ���ǣ�������| A�� | ��һ�������У�����F����������ֵһ������F�� | |
| B�� | ������������������������� | |
| C�� | ���������У�ˮƽ����������ͬ | |
| D�� | �ڶ��������У�������ˮƽ����F��ĺ����Ĺ��������Ӻ��С |
�鿴�𰸺ͽ���>>
��Ŀ���������� ��Դ�� ���ͣ�ѡ����
 һ����Ϊm1Բ�����ڹ⻬�Ĺ̶���ֱ���ϣ�һϸ����һ����Բ�����ӣ���һ��ͨ����������һ����Ϊm2��������������ͼ��ʾ��������B���ɾ�ֹ��ʼ�ͷţ��˶�����͵�B1ʱ��Բ����λ��A�˶���λ��A1����֪Բ�������˶��Ĺ������ܴﵽ����ߵ�ΪA2���������ٶ�Ϊg������ϸ���붨���ֵ����������������һ��Ħ����������
һ����Ϊm1Բ�����ڹ⻬�Ĺ̶���ֱ���ϣ�һϸ����һ����Բ�����ӣ���һ��ͨ����������һ����Ϊm2��������������ͼ��ʾ��������B���ɾ�ֹ��ʼ�ͷţ��˶�����͵�B1ʱ��Բ����λ��A�˶���λ��A1����֪Բ�������˶��Ĺ������ܴﵽ����ߵ�ΪA2���������ٶ�Ϊg������ϸ���붨���ֵ����������������һ��Ħ����������| A�� | ����Ӿ�ֹ�ͷŵ���һ���˶�����͵�B1�����У�ϸ�������������һֱС����������� | |
| B�� | Բ���������˶��Ĺ����У����ٶ�����λ����A1λ�� | |
| C�� | Բ����Aλ���˶���A2λ�ã�����A��A2λ�ã��Ĺ����У�������ٶ�һֱС��Բ�����ٶ� | |
| D�� | ������B���ͷ�ʱ��ϸ������ֱ�˼�ļн�Ϊ�ȣ��������ͷ�˲�䣬Բ���ļ��ٶȴ�СΪ$\frac{{m}_{2}gcos��-{m}_{1}g}{{m}_{1}}$ |
�鿴�𰸺ͽ���>>
��Ŀ���������� ��Դ�� ���ͣ�ѡ����
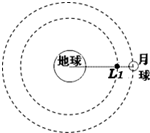 �����������������һ���������յ�L1������λ�ڸõ��С�����ڵ�������������Ĺ�ͬ�����£������Ըպñ�����������������λ�ò��䣬�Ӷ�������һ������ͬ�������Ƶ����˶�����ͼ��ʾ�������������������յ�L1�����ԣ��ڸõ���һ̽����תվ������a1��a2��a3�ֱ��ʾ����תվ������͵���ͬ�������Ƶ���ת�����ļ��ٶȴ�С��������
�����������������һ���������յ�L1������λ�ڸõ��С�����ڵ�������������Ĺ�ͬ�����£������Ըպñ�����������������λ�ò��䣬�Ӷ�������һ������ͬ�������Ƶ����˶�����ͼ��ʾ�������������������յ�L1�����ԣ��ڸõ���һ̽����תվ������a1��a2��a3�ֱ��ʾ����תվ������͵���ͬ�������Ƶ���ת�����ļ��ٶȴ�С��������| A�� | a2��a3��a1 | B�� | a2��a1��a3 | C�� | a3��a1��a2 | D�� | a3��a2��a1 |
�鿴�𰸺ͽ���>>
��Ŀ���������� ��Դ�� ���ͣ������

�鿴�𰸺ͽ���>>
��Ŀ���������� ��Դ�� ���ͣ�ѡ����
| A�� | ��ѹ��ѹ����ԭ����Ȧ����֮��Ϊ$\frac{{n}_{1}}{{n}_{2}}=\frac{{U}_{1}}{U}$ | |
| B�� | ��ѹ��ѹ����ԭ����Ȧ����֮��Ϊ$\frac{{n}_{3}}{{n}_{4}}=\frac{U}{{U}_{2}}$ | |
| C�� | ���������ʧ�Ĺ���P=$\frac{{U}^{2}}{R}$ | |
| D�� | ��U1���ֲ��䣬�õ�������ʱ��U2����� |
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com