
分析 根据万有引力提供向心力得出中心天体质量与周期和轨道半径的关系,从而得出太阳和地球的质量之比.
解答 解:根据$G\frac{Mm}{{r}^{2}}=m\frac{4{π}^{2}r}{{T}^{2}}$得,
中心天体的质量M=$\frac{4{π}^{2}r}{{T}^{2}}$.
因为地球的轨道半径和月球的轨道半径之比为r1:r2=400:1,
周期之比为T1:T2=14:1,
则太阳和地球的质量之比为$\frac{{M}_{太}}{{M}_{地}}=\frac{{{r}_{1}}^{3}{{T}_{2}}^{2}}{{{r}_{2}}^{3}{{T}_{1}}^{2}}=3×1{0}^{5}$,
则太阳质量约为地球质量的3×105倍.
答:太阳的质量是地球质量的3×105倍.
点评 解决本题的关键掌握万有引力提供向心力这一理论,知道运用这一理论只能求出中心天体的质量,不能求解环绕天体的质量.


 小学数学口算题卡脱口而出系列答案
小学数学口算题卡脱口而出系列答案 优秀生应用题卡口算天天练系列答案
优秀生应用题卡口算天天练系列答案 浙江之星课时优化作业系列答案
浙江之星课时优化作业系列答案科目:高中物理 来源: 题型:填空题
查看答案和解析>>
科目:高中物理 来源: 题型:解答题
 如图所示,两个气缸内封有一定质量的气体,两活塞通过细杆连接,活塞截面积SB=2SA,外界大气压为1atm,当活塞平衡时,A缸内气体压强为PA=2atm,则B缸内气体压强PB为多大?(不计摩擦)
如图所示,两个气缸内封有一定质量的气体,两活塞通过细杆连接,活塞截面积SB=2SA,外界大气压为1atm,当活塞平衡时,A缸内气体压强为PA=2atm,则B缸内气体压强PB为多大?(不计摩擦)查看答案和解析>>
科目:高中物理 来源: 题型:解答题
 如图所示,质量为M的物体静止于光滑水平面上,其上有一个半径为R的光滑半圆形轨道,现把质量为m的小球自轨道左侧最高点静止释放,试计算:白球运动的最高点的过程中,轨道产生的位移大小是多少?
如图所示,质量为M的物体静止于光滑水平面上,其上有一个半径为R的光滑半圆形轨道,现把质量为m的小球自轨道左侧最高点静止释放,试计算:白球运动的最高点的过程中,轨道产生的位移大小是多少?查看答案和解析>>
科目:高中物理 来源: 题型:解答题
查看答案和解析>>
科目:高中物理 来源: 题型:解答题
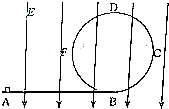 如图所示,AB为一绝缘的水平直轨道,BCDF为一绝缘的光滑圆形轨道,B为圆轨道最低点,竖直放置在竖直方向的匀强电场中,BCDF是半径为R的圆形轨道,今有质量为m的带正电的小滑块(可视为质点)以一初速度v0由A点开始沿轨道向右运动,小滑块恰好能沿竖直圆轨道做完整的圆周运动,已知小滑块与AB轨道间的动摩擦因数为μ,A与B之间距离为L,电场强度E=$\frac{mg}{q}$,重力加速度为g,求:
如图所示,AB为一绝缘的水平直轨道,BCDF为一绝缘的光滑圆形轨道,B为圆轨道最低点,竖直放置在竖直方向的匀强电场中,BCDF是半径为R的圆形轨道,今有质量为m的带正电的小滑块(可视为质点)以一初速度v0由A点开始沿轨道向右运动,小滑块恰好能沿竖直圆轨道做完整的圆周运动,已知小滑块与AB轨道间的动摩擦因数为μ,A与B之间距离为L,电场强度E=$\frac{mg}{q}$,重力加速度为g,求:查看答案和解析>>
科目:高中物理 来源: 题型:选择题
 如图所示,一带铁芯线圈置于竖直悬挂的闭合铝框右侧,与线圈相连的导线abcd内有水平向里变化的磁场下列哪种变化磁场可使铝框向左偏离( )
如图所示,一带铁芯线圈置于竖直悬挂的闭合铝框右侧,与线圈相连的导线abcd内有水平向里变化的磁场下列哪种变化磁场可使铝框向左偏离( )| A. |  | B. |  | C. |  | D. |  |
查看答案和解析>>
科目:高中物理 来源: 题型:选择题
| A. | 2$\sqrt{2}$v | B. | $\sqrt{2}$v | C. | 2v | D. | $\frac{v}{2}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com