
 如图所示,在空间中取直角坐标系Oxy,在第一象限内平行于y轴的虚线MN与y轴距离为d,从y轴到MN之间的区域充满一个沿y轴正方向的匀强电场,场强大小为E.初速度可以忽略的电子经过另一个电势差为U的电场加速后,从y轴上的A点以平行于x轴的方向射入第一象限区域,A点坐标为(0,h).已知电子的电量为e,质量为m,若加速电场的电势差U>$\frac{E{d}^{2}}{4h}$,电子的重力忽略不计,求:
如图所示,在空间中取直角坐标系Oxy,在第一象限内平行于y轴的虚线MN与y轴距离为d,从y轴到MN之间的区域充满一个沿y轴正方向的匀强电场,场强大小为E.初速度可以忽略的电子经过另一个电势差为U的电场加速后,从y轴上的A点以平行于x轴的方向射入第一象限区域,A点坐标为(0,h).已知电子的电量为e,质量为m,若加速电场的电势差U>$\frac{E{d}^{2}}{4h}$,电子的重力忽略不计,求:分析 (1)电子在沿x轴方向做匀速运动,即可求得运动时间,在电场方向做匀加速运动,由运动学公式及可求得速度;
(2)电子射入第一象限的电场中做类平抛运动,水平方向做匀速直线运动,竖直方向做初速度为零的匀加速直线运动,根据牛顿第二定律和运动学公式结合求解出出电场点的坐标,电子离开电场后水平、竖直方向上都做匀速运动,先求出电子射出P点的速度,再由位移公式求解电子经过x轴时离坐标原点O的距离.
解答 解:(1)由 eU=$\frac{1}{2}$mv02
得电子进入偏转电场区域的初速度v0=$\sqrt{\frac{2eU}{m}}$
设电子从MN离开,则电子从A点进入到离开匀强电场区域的时间t=$\frac{d}{v0}$=$d\sqrt{\frac{m}{2eU}}$;
y=$\frac{1}{2}$at2=$\frac{E{d}^{2}}{4U}$
因为加速电场的电势差U>$\frac{E{d}^{2}}{4h}$,说明y<h,说明以上假设正确,
所以vy=at=$\frac{eE}{m}$×d$\sqrt{\frac{m}{2eU}}$=$\frac{eEd}{m}\sqrt{\frac{m}{2eU}}$
离开时的速度v=$\sqrt{{v}_{0}^{2}{+v}_{y}^{2}}=\sqrt{\frac{2eU}{m}+\frac{e{E}^{2}{d}^{2}}{2mU}}$
(2)设电子离开电场后经过时间t′到达x轴,在x轴方向上的位移为x′,则
x′=v0t′
y′=h-y=h-$\frac{{v}_{y}}{2}$t=vyt′
则 l=d+x′=d+v0t′=d+v0($\frac{h}{vy}$-$\frac{t}{2}$)=d+$\frac{v0}{vy}$h-$\frac{d}{2}$=$\frac{d}{2}$+$\frac{v0}{vy}$h
代入解得 l=$\frac{d}{2}$+$\frac{2hU}{Ed}$
答:(1)若加速电场的电势差U>$\frac{E{d}^{2}}{4h}$,则电子从A点进入电场到离开该电场区域所经历的时间t为$d\sqrt{\frac{m}{2eU}}$,离开电场区域时的速度v为$\sqrt{\frac{2eU}{m}+\frac{e{E}^{2}{d}^{2}}{2mU}}$;
(2)电子经过x轴时离坐标原点O的距离l为$\frac{d}{2}$+$\frac{2hU}{Ed}$.
点评 本题是带电粒子在匀强电场中加速和偏转结合的问题,能熟练运用运动的分解法研究类平抛运动,结合几何知识进行求解.


科目:高中物理 来源: 题型:解答题
 某同学设计了一个研究平抛运动的实验.实验装置示意图如图所示,A是一块平面木板,在其上等间隔地开凿出一组平行的插槽(图1中P0P0′、P1P1′…),槽间距离均为d.把覆盖复写纸的白纸铺贴在硬板B上.实验时依次将B板插入A板的各插槽中,每次让小球从斜轨的同一位置由静止释放.每打完一点后,把B板插入后一槽中.实验得到小球在白纸上打下的若干痕迹点,如图2所示.
某同学设计了一个研究平抛运动的实验.实验装置示意图如图所示,A是一块平面木板,在其上等间隔地开凿出一组平行的插槽(图1中P0P0′、P1P1′…),槽间距离均为d.把覆盖复写纸的白纸铺贴在硬板B上.实验时依次将B板插入A板的各插槽中,每次让小球从斜轨的同一位置由静止释放.每打完一点后,把B板插入后一槽中.实验得到小球在白纸上打下的若干痕迹点,如图2所示.查看答案和解析>>
科目:高中物理 来源: 题型:解答题
查看答案和解析>>
科目:高中物理 来源: 题型:多选题
| A. | vA=4m/s,vB=4m/s | B. | vA=2m/s,vB=5m/s | ||
| C. | vA=-4m/s,vB=6m/s | D. | vA=7m/s,vB=2.5m/s | ||
| E. | vA=3m/s,vB=4.5m/s |
查看答案和解析>>
科目:高中物理 来源: 题型:选择题
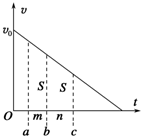 一个物体以初速度v0沿光滑斜面向上运动,其速度v随时间t变化的规律如图所示,在连续两段时间m和n内对应面积均为S,设经过b时刻的加速度和速度分别为a和vb,则( )
一个物体以初速度v0沿光滑斜面向上运动,其速度v随时间t变化的规律如图所示,在连续两段时间m和n内对应面积均为S,设经过b时刻的加速度和速度分别为a和vb,则( )| A. | a=$\frac{2(m+n)S}{(m-n)mn}$ | B. | a=$\frac{2(m-n)S}{(m+n)mn}$ | C. | vb=$\frac{(m+n)S}{mn}$ | D. | vb=$\frac{({m}^{2}+{n}^{2})S}{mn}$ |
查看答案和解析>>
科目:高中物理 来源: 题型:解答题

查看答案和解析>>
科目:高中物理 来源: 题型:选择题
 如图所示,一细束a光和一细束b光平行射到同一个三棱镜上,经折射后交于光屏上的同一个点M,若用n1和n2分别表示三棱镜对a光和b光的折射率,用v1和v2分别表示a光和b光在三棱镜中的光速,用λ1和λ2分别表示a光和b光在三棱镜中的波长,下列说法正确的是( )
如图所示,一细束a光和一细束b光平行射到同一个三棱镜上,经折射后交于光屏上的同一个点M,若用n1和n2分别表示三棱镜对a光和b光的折射率,用v1和v2分别表示a光和b光在三棱镜中的光速,用λ1和λ2分别表示a光和b光在三棱镜中的波长,下列说法正确的是( )| A. | n1>n2,λ1<λ2,v1<v2 | B. | n1<n2,λ1<λ2,v1<v2 | ||
| C. | n1<n2,λ1>λ2,v1<v2 | D. | n1>n2,λ1<λ2,v1>v2 |
查看答案和解析>>
科目:高中物理 来源: 题型:多选题
| A. | 运转轨道平面与赤道平面是重合的 | |
| B. | 轨道平面与某经线所在平面是重合的 | |
| C. | 轨道平面与赤道以外的某纬线所在平面是重合的 | |
| D. | 轨道平面通过地球球心,但平面与任一纬线和经线均不重合 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com