
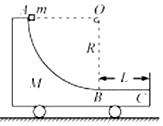
 如图,质量为M的小车静止在光滑的水平面上,小车AB段是半径为R的四分之一圆弧光滑轨道,BC段是长为L的水平粗糙轨道,两段轨道相切于B点,一质量为m的滑块在小车上从A点静止开始沿轨道滑下,然后滑入BC轨道,最后从C点滑出小车,已知滑块质量与小车质量间的关系为2m=M,滑块与轨道BC间的动摩擦因数为μ,重力加速度为g.求:
如图,质量为M的小车静止在光滑的水平面上,小车AB段是半径为R的四分之一圆弧光滑轨道,BC段是长为L的水平粗糙轨道,两段轨道相切于B点,一质量为m的滑块在小车上从A点静止开始沿轨道滑下,然后滑入BC轨道,最后从C点滑出小车,已知滑块质量与小车质量间的关系为2m=M,滑块与轨道BC间的动摩擦因数为μ,重力加速度为g.求:分析 (1)滑块到达B点时小车速度最大,小车与滑块组成的系统水平方向动量守恒,应用动量守恒定律与能量守恒定律可以求出小车的最大速度.
(2)滑块从A运动到C的过程中,小车与滑块组成的系统水平方向动量守恒,应用动量守恒定律与能量守恒定律可以求出小车的最大速度.
(3)由牛顿第二定律求出小车的加速度,然后应用速度位移公式求出小车的位移.
解答 解:(1)滑块到达B点时,小车的速度最大,
小车与滑块组成的系统水平方向动量守恒,
以向右为正方向,由动量守恒定律得:mv-Mvm=0,
滑块从A到B过程,由能量守恒定律得:mgR=$\frac{1}{2}$mv2+$\frac{1}{2}$Mvm2,
解得:vm=$\sqrt{\frac{1}{3}gR}$;
(2)滑块到C处过程小车与滑块组成的系统水平方向动量守恒,
以向右为正方向,由动量守恒定律得:mv′-Mv″=0,
由能量守恒定律得:mgR=$\frac{1}{2}$mv′2+$\frac{1}{2}$Mv″2+μmgL,
解得:v″=$\sqrt{\frac{1}{3}gR-\frac{1}{3}μgL}$;
(3)滑块从B到C过程,小车的加速度:a=$\frac{μmg}{M}$=$\frac{1}{2}$μg,
由匀变速直线运动的速度位移公式得:vm2-v″2=2as,解得:s=$\frac{1}{3}$L;
答:(1)滑块运动过程中,小车的最大速度vm为$\sqrt{\frac{1}{3}gR}$.
(2)当滑块运动至C点时,小车的速度大小为$\sqrt{\frac{1}{3}gR-\frac{1}{3}μgL}$.
(3)滑块从B到C运动过程中,小车的位移大小s为$\frac{1}{3}$L.
点评 该题主要考查系统水平方向动量守恒和能量守恒的问题,求解两物体间的相对位移,往往根据平均速度研究.也可以根据题目提供的特殊的条件:在任一时刻滑块相对地面速度的水平分量是小车速度大小的2倍,不使用动量守恒定律.


科目:高中物理 来源: 题型:多选题
 如图所示,质量均为1kg的两个物体A、B放在水平地面上相距9m,它们与水平地面的动摩擦因数均为μ=0.2.现使它们分别以大小vA=6m/s和vB=2m/s的初速度同时相向滑行,不计物体的大小,取g=10m/s2.则( )
如图所示,质量均为1kg的两个物体A、B放在水平地面上相距9m,它们与水平地面的动摩擦因数均为μ=0.2.现使它们分别以大小vA=6m/s和vB=2m/s的初速度同时相向滑行,不计物体的大小,取g=10m/s2.则( )| A. | 它们经过2s相遇 | B. | 它们经过4s相遇 | ||
| C. | 它们在距离物体A出发点8m 处相遇 | D. | 它们在距离物体A出发点6m 处相遇 |
查看答案和解析>>
科目:高中物理 来源: 题型:填空题
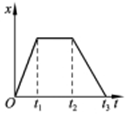 一质点的x-t图象如图所示,在t1~t2时间内质点静止(填是什么运动状态),在O~t1时间内的速度方向和t2~t3时间内的速度方向相反(填“相同”或“相反”).
一质点的x-t图象如图所示,在t1~t2时间内质点静止(填是什么运动状态),在O~t1时间内的速度方向和t2~t3时间内的速度方向相反(填“相同”或“相反”).查看答案和解析>>
科目:高中物理 来源: 题型:实验题
 测量干电池的电动势和内电阻,备有下列器材:
测量干电池的电动势和内电阻,备有下列器材:查看答案和解析>>
科目:高中物理 来源: 题型:多选题
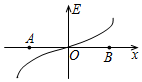 空间存在一沿x轴的静电场,电场强度E随x变化的关系如图所示,图象关于坐标原点对称,A、B是x轴关于原点对称的两点.下列说法中错误的是( )
空间存在一沿x轴的静电场,电场强度E随x变化的关系如图所示,图象关于坐标原点对称,A、B是x轴关于原点对称的两点.下列说法中错误的是( )| A. | 电子在A、B两点的电势能相等 | |
| B. | 电子在A、B两点的加速度方向相反 | |
| C. | 电子从A点由静止释放后的运动轨迹可能是曲线 | |
| D. | 取无穷远处电势为零,则O点处电势亦为零 |
查看答案和解析>>
科目:高中物理 来源: 题型:多选题
| A. | 力学中为了研究方便,任何物体任何时候都可以看成质点,质点是理想化模型 | |
| B. | 在推导匀变速直线运动位移公式时,把整个运动过程划分成很多小段,每一小段近似看作匀速直线运动,再把各小段位移相加,这里运用了假设法 | |
| C. | 用比值法定义的物理概念在物理学中占有相当大的比例,例如,加速度a=$\frac{△v}{△t}$和速度v=$\frac{△x}{△t}$都是采用比值法定义的 | |
| D. | 根据速度定义式v=$\frac{△x}{△t}$,当△t非常小时,$\frac{△x}{△t}$就可以表示物体在t时刻的瞬时速度,这里运用了极限思维法 |
查看答案和解析>>
科目:高中物理 来源: 题型:多选题
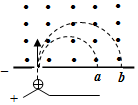 如图,质量相同而电量不同的两个正电荷,从静止开始,经过同一加速电场后,垂直界面进入同一匀强磁场,最后分别打在a、b两点,不计粒子重力,由图可知( )
如图,质量相同而电量不同的两个正电荷,从静止开始,经过同一加速电场后,垂直界面进入同一匀强磁场,最后分别打在a、b两点,不计粒子重力,由图可知( )| A. | 打在a点的粒子速度大 | B. | 打在b点的粒子速度大 | ||
| C. | a的电荷量大于b的电荷量 | D. | a、b在磁场中运动的时间相同 |
查看答案和解析>>
科目:高中物理 来源: 题型:选择题
| A. | 当l不变,S增大一倍时 | B. | 当S不变,长度l增大一倍时 | ||
| C. | 当长度l和面积S都减为原来一半时 | D. | 当l和横截面半径都增大一倍时 |
查看答案和解析>>
科目:高中物理 来源: 题型:实验题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com