
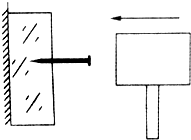
 木匠用质量为m0的钉锤击打质量为m(m0≥m)的钉子,把木条钉牢在竖直的木墙上.在钉人某一颗钉子时,测得第一次敲打使钉子进入的深度为L,如图所示.
木匠用质量为m0的钉锤击打质量为m(m0≥m)的钉子,把木条钉牢在竖直的木墙上.在钉人某一颗钉子时,测得第一次敲打使钉子进入的深度为L,如图所示.| kx1+kx2 | 2 |
. |
| F |
| 1 |
| 2 |
. |
| F |
| ||
| 2L(m0+m) |
| v | 2 0 |
. |
| F2 |
| kL+k(L+L2) |
| 2 |
| k(2L+L2) |
| 2 |
| 2L+L2 |
| 2 |
| L |
| 2 |
| 2 |
| 3 |
| 2 |
| N |
| N |
. |
| F |
| ||
| 2L(m0+m) |
| v | 2 0 |
| 2 |


湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com