
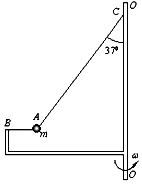
 如图所示,装置BO′O可绕竖直轴OO′转动,可视为质点的小球A与两细线连接后分别系于B、C两点,装置静止时细线AB水平,细线AC与竖直方向的夹角θ=37°.已知小球的质量m=1kg,细线AC 长L=1m,B点距C点的水平和竖直距离相等.(g取10m/s2,sin37°=0.6,cos37°=0.8,结果可用根式表达)
如图所示,装置BO′O可绕竖直轴OO′转动,可视为质点的小球A与两细线连接后分别系于B、C两点,装置静止时细线AB水平,细线AC与竖直方向的夹角θ=37°.已知小球的质量m=1kg,细线AC 长L=1m,B点距C点的水平和竖直距离相等.(g取10m/s2,sin37°=0.6,cos37°=0.8,结果可用根式表达)分析 (1)由静止时受力平衡求得细线AB上的张力,进而求得匀速转动时的向心力,从而求得加速度;
(2)由几何关系求得半径,进而根据受力求得向心力,从而求得加速度.
解答 解:(1)细线AB上张力恰为零时有:小球所受合外力为mgtan37°,应用牛顿第二定律可得:$mgtan37°=m{{ω}_{1}}^{2}Lsin37°$,所以,${ω}_{1}=\sqrt{\frac{mgtan37°}{mLsin37°}}=\sqrt{\frac{g}{Lcos37°}}=\sqrt{\frac{10}{1×0.8}}rad/s$=$\frac{5\sqrt{2}}{2}rad/s$;
(2)装置静止时细线AB水平,细线AC与竖直方向的夹角θ=37°,B点距C点的水平和竖直距离相等,所以,B点到OO′的距离为d=Lcos37°=0.8m;
若装置以ω2匀速转动时,细线AB刚好竖直且张力为零,则细线与OO′之间的夹角为θ,那么,$sinθ=\frac{d}{L}=0.8$,
所以,此时合外力F=mgtanθ,应用牛顿第二定律可得:$F=mgtanθ=m{{ω}_{2}}^{2}d$,
所以,${ω}_{2}=\sqrt{\frac{mgtanθ}{md}}=\sqrt{\frac{gtanθ}{d}}=\sqrt{\frac{10×\frac{4}{3}}{0.8}}rad/s$=$\frac{10\sqrt{6}}{6}rad/s$;
答:(1)若装置匀速转动的角速度为ω1,细线AB上的张力为零而细线AC与竖直方向夹角仍为37°,则角速度ω1的大小为$\frac{5\sqrt{2}}{2}rad/s$;
(2)若装置以ω2匀速转动时,细线AB刚好竖直且张力为零,则此时角速度ω2的大小为$\frac{10\sqrt{6}}{6}rad/s$.
点评 在求解匀速圆周运动的相关物理量时,一般根据受力分析求得合外力,然后求得向心力,再利用向心力公式求解速度、半径、周期等物理量.


 阅读快车系列答案
阅读快车系列答案科目:高中物理 来源: 题型:多选题
 如图所示,水平光滑地面上停放着一辆质量为M的小车,小车左端靠在竖直墙壁上,其左侧半径为R的四分之一圆弧轨道AB是光滑的,轨道最低点B与水平轨道BC相切,整个轨道处于同一竖直平面内.将质量为m的物块(可视为质点)从A点无初速释放,物块沿轨道滑行至轨道末端C处恰好没有滑出.重力加速度为g,空气阻力可忽略不计.关于物块从A位置运动至C位置的过程,下列说法中正确的是( )
如图所示,水平光滑地面上停放着一辆质量为M的小车,小车左端靠在竖直墙壁上,其左侧半径为R的四分之一圆弧轨道AB是光滑的,轨道最低点B与水平轨道BC相切,整个轨道处于同一竖直平面内.将质量为m的物块(可视为质点)从A点无初速释放,物块沿轨道滑行至轨道末端C处恰好没有滑出.重力加速度为g,空气阻力可忽略不计.关于物块从A位置运动至C位置的过程,下列说法中正确的是( )| A. | 在这个过程中,小车和物块构成的系统水平方向动量守恒 | |
| B. | 在这个过程中,物块克服摩擦力所做的功为mgR | |
| C. | 在这个过程中,摩擦力对小车所做的功为$\frac{MgR{m}^{2}}{(M+m)^{2}}$ | |
| D. | 在这个过程中,由于摩擦生成的热量为$\frac{mMgR}{M+m}$ |
查看答案和解析>>
科目:高中物理 来源: 题型:填空题
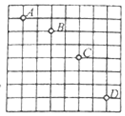 某宇航员登上没有空气的未知星球后,将一个小物体沿水平方向抛出,并采用频闪照相的方法记录下小物体在运动过程中的4个位置A、B、C、D,如图所示,已知两次曝光的时间间隔为0.1s,照片中每一小方格边长为5cm.则可知小物体抛出瞬间的速度为1m/s,该星球表面的重力加速度为5m/s2.若已知该星球的半径为地球半径的$\frac{1}{2}$,地球表面重力加速度取10m/s2,地球的第一宇宙速度为7.9km/s,则该星球的第一宇宙速度为3.95km/s.
某宇航员登上没有空气的未知星球后,将一个小物体沿水平方向抛出,并采用频闪照相的方法记录下小物体在运动过程中的4个位置A、B、C、D,如图所示,已知两次曝光的时间间隔为0.1s,照片中每一小方格边长为5cm.则可知小物体抛出瞬间的速度为1m/s,该星球表面的重力加速度为5m/s2.若已知该星球的半径为地球半径的$\frac{1}{2}$,地球表面重力加速度取10m/s2,地球的第一宇宙速度为7.9km/s,则该星球的第一宇宙速度为3.95km/s.查看答案和解析>>
科目:高中物理 来源: 题型:选择题
| A. | 它的加速度为零 | B. | 它所受合力为零 | ||
| C. | 它所受合外力大小方向均不变 | D. | 它所受合外力大小不变,方向改变 |
查看答案和解析>>
科目:高中物理 来源: 题型:选择题
| A. | 车轮与路面间的静摩擦力 | B. | 重力和支持力的合力 | ||
| C. | 发动机的牵引力 | D. | 空气的阻力 |
查看答案和解析>>
科目:高中物理 来源: 题型:实验题
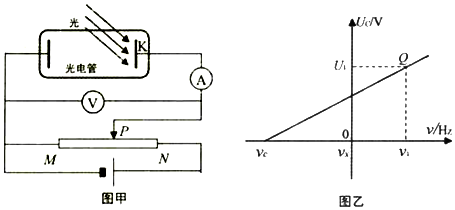 美国物理学家密立根利用图甲所示的电路研究金属的遏止电压UC与入射光频率v的关系,描绘出图乙中的图象,由此算出普朗克常量h.电子电量用e表示,回答下列问题:
美国物理学家密立根利用图甲所示的电路研究金属的遏止电压UC与入射光频率v的关系,描绘出图乙中的图象,由此算出普朗克常量h.电子电量用e表示,回答下列问题:查看答案和解析>>
科目:高中物理 来源: 题型:解答题
查看答案和解析>>
科目:高中物理 来源: 题型:选择题
| A. | 只有体积很小的物体才能看作质点 | |
| B. | 在太空中进行飞船对接的宇航员观察该飞船,不可把飞船看作质点 | |
| C. | 质点是一个理想化的模型,实际并不存在,所以,引入这个概念没有多大意义 | |
| D. | 从地球上的控制中心跟踪观察在太空中飞行的宇宙飞船,不可把飞船看作质点 |
查看答案和解析>>
科目:高中物理 来源: 题型:多选题
| A. | 因为布朗运动的激烈程度跟温度有关,所以布朗运动又称为热运动 | |
| B. | 随着分子间距增大,分子间引力和斥力均减小,但分子势能不一定减小 | |
| C. | 对于一定质量的理想气体,气体压强和体积都增大时,其分子平均动能增大 | |
| D. | 在空气的绝对湿度相同的情况下,白天一般比夜晚的相对湿度大 | |
| E. | 在油膜法估测分子大小的实验中,如果有油酸未完全散开会使测量结果偏大 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com