
| A�� | �������е��ٶȴ�С������������ | |
| B�� | �������е��ٶȴ�С�����뾶�ɷ��� | |
| C�� | �������е����ļ��ٶȵĴ�С������������ | |
| D�� | ����֮��ľ�����Ա�ʾΪ$\root{3}{\frac{G��M+m��{T}^{2}}{4{��}^{2}}}$ |
���� ˫�ǿ��������������ṩ��������������ͬ�Ľ��ٶȣ�����v=��r��v=$\frac{2��r}{T}$����ABѡ��������е����ļ��ٶ�a=$\frac{F}{m}$���������������ṩ�����������ڹ�ʽ��ʽ���L��
��� �⣺A����˫��ϵͳ����������������֮������������ṩ��������������Χ�������ϵ�ijһ�̶���������Բ���˶��Ľ��ٶ�Ϊ�أ��ɵ�M��v1=m��v2����A����
B����v=$\frac{2��r}{T}$�ɵ�$\frac{{v}_{1}}{{r}_{1}}$=$\frac{{v}_{2}}{{r}_{2}}$����B����
C���������е����ļ��ٶ�a=$\frac{F}{m}$����C����
D��������֮��ľ���ΪL����G$\frac{Mm}{{L}^{2}}$=Mr1��$\frac{2��}{T}$��2��G$\frac{Mm}{{L}^{2}}$=mr2��$\frac{2��}{T}$��2��L=r1+r2���������L=$\root{3}{\frac{G��M+m��{T}^{2}}{4{��}^{2}}}$����D��ȷ��
��ѡ��D
���� ������Ҫ������˫��ϵͳ���ص㣬֪��˫�ǿ��������������ṩ��������������ͬ�Ľ��ٶȣ��ѶȲ������ڻ����⣮



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ���������� ��Դ�� ���ͣ�ѡ����
 �������ȵĸֹܣ�һ��֧��ˮƽ�����ϣ���һ�˱���ֱ���������ţ����ھ�ֹ״̬�����ڸֹ�������������з�����ȷһ���ǣ�������
�������ȵĸֹܣ�һ��֧��ˮƽ�����ϣ���һ�˱���ֱ���������ţ����ھ�ֹ״̬�����ڸֹ�������������з�����ȷһ���ǣ�������| A�� | ��ֱ���µ�������������ֱ���ϵ����� | |
| B�� | ��ֱ���µ�������������ֱ���ϵ�֧���� | |
| C�� | ��ֱ���µ�������������ֱ���ϵ������͵�����ֱ���ϵ�֧���� | |
| D�� | ��ֱ���µ�������������ֱ���ϵ�������������ֱ���ϵ�֧�����͵���ˮƽĦ���� |
�鿴�𰸺ͽ���>>
��Ŀ���������� ��Դ�� ���ͣ������
 ��ͼ��ʾ��һ�����쳤�������϶�������O�㣬�¶�ϵһ����m=2.0kg ��С���ֽ�С������A�㣨��������ֱ���ɾ�ֹ�ͷţ���������B��ʱ��ǡ�ñ����ϣ�С��ƽ������ˮƽ�����ϵ�C�㣮�����ϵ�D����OB��ͬһ��ֱ���ϣ���֪����L=1.0m��B����ظ߶�H=5.0m����AOB=60�㣬�������ٶ�gȡ10m/s2�����ƿ���Ӱ�죬��
��ͼ��ʾ��һ�����쳤�������϶�������O�㣬�¶�ϵһ����m=2.0kg ��С���ֽ�С������A�㣨��������ֱ���ɾ�ֹ�ͷţ���������B��ʱ��ǡ�ñ����ϣ�С��ƽ������ˮƽ�����ϵ�C�㣮�����ϵ�D����OB��ͬһ��ֱ���ϣ���֪����L=1.0m��B����ظ߶�H=5.0m����AOB=60�㣬�������ٶ�gȡ10m/s2�����ƿ���Ӱ�죬���鿴�𰸺ͽ���>>
��Ŀ���������� ��Դ�� ���ͣ�ѡ����
| A�� | �κ�����£����渽���������ܵ�������һ�����ڵ��������֮����������� | |
| B�� | �κ�����£����渽���������ܵ���������һ��ָ����� | |
| C�� | �κ�����£����������������ٶȶ����Ա�ʾΪg=G$\frac{M}{{R}^{2}}$��ʽ��MΪ�����������RΪ����İ뾶 | |
| D�� | ֻ���ڲ�����������תʱ�����������������ٶȲſ��Ա�ʾΪg=G$\frac{M}{{R}^{2}}$��ʽ��MΪ�����������RΪ����İ뾶 |
�鿴�𰸺ͽ���>>
��Ŀ���������� ��Դ�� ���ͣ���ѡ��
| A�� | ���������ٶȵĴ�С�������ɷ��� | |
| B�� | ���������ٶȵĴ�С�����뾶�ɷ��� | |
| C�� | �������е����ļ��ٶȵĴ�С�������ɷ��� | |
| D�� | ������������ܵ����������ϴ� |
�鿴�𰸺ͽ���>>
��Ŀ���������� ��Դ�� ���ͣ�ѡ����
| A�� | ������������3J | B�� | �������ܼ���3J | C�� | ���ܼ���1J | D�� | ��������3J |
�鿴�𰸺ͽ���>>
��Ŀ���������� ��Դ�� ���ͣ���ѡ��
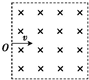 ����ͼ��ʾ���������������д�ֱֽ���������ǿ�ų���һ���Ⱥ���ͬ�Ҵ�ͬ�ֵ�ɵ��������ӱ߽��ϵ�O���ش�ֱ�ڴų��ͱ߽�ķ����Բ�ͬ��������ų��������������������Ӽ������ã����з�����ȷ���ǣ�������
����ͼ��ʾ���������������д�ֱֽ���������ǿ�ų���һ���Ⱥ���ͬ�Ҵ�ͬ�ֵ�ɵ��������ӱ߽��ϵ�O���ش�ֱ�ڴų��ͱ߽�ķ����Բ�ͬ��������ų��������������������Ӽ������ã����з�����ȷ���ǣ�������| A�� | �����ٶ���ͬ�����ӣ���켣һ����ͬ | |
| B�� | �����ӵĹ켣��ͬ����������������ڴų����˶���ʱ�䳤 | |
| C�� | �����ڴų����˶���ʱ��Խ�̣��������ٶ�Խ�� | |
| D�� | �������ڴų����˶���ʱ����ͬ���������ٶ�һ����ͬ |
�鿴�𰸺ͽ���>>
��Ŀ���������� ��Դ�� ���ͣ�ѡ����
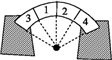 ��ͼ��ʾ�����Ŀ���ͬ�ļ��ʯ���ݳ�Բ���ε�ʯ�������е�3��4��̶��ڵػ��ϣ���1��2���ĽӴ�������ֱ�ģ�ÿ��ʯ��������������е�Բ�ĽǾ�Ϊ30�㣬ÿ��ʯ���������ΪG������ʯ����Ħ�������Ժ��Բ��ƣ����1��2��ʯ������������СΪ
��ͼ��ʾ�����Ŀ���ͬ�ļ��ʯ���ݳ�Բ���ε�ʯ�������е�3��4��̶��ڵػ��ϣ���1��2���ĽӴ�������ֱ�ģ�ÿ��ʯ��������������е�Բ�ĽǾ�Ϊ30�㣬ÿ��ʯ���������ΪG������ʯ����Ħ�������Ժ��Բ��ƣ����1��2��ʯ������������СΪ| A�� | $\frac{1}{2}$G | B�� | $\frac{\sqrt{3}}{2}$G | C�� | $\frac{\sqrt{3}}{3}$G | D�� | $\sqrt{3}$G |
�鿴�𰸺ͽ���>>
��Ŀ���������� ��Դ�� ���ͣ�ѡ����
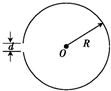 ��ͼ��ʾ���뾶ΪR������Բ���Ͼ��ȷֲ��ŵ����ΪQ�ĸ���ɣ�Բ�������һСȱ�ڣ������Ϊd��d����R������Բ��O��һ�������Ϊ+q�ĵ������ܵĵ糡����������
��ͼ��ʾ���뾶ΪR������Բ���Ͼ��ȷֲ��ŵ����ΪQ�ĸ���ɣ�Բ�������һСȱ�ڣ������Ϊd��d����R������Բ��O��һ�������Ϊ+q�ĵ������ܵĵ糡����������| A�� | ��СΪ$\frac{kdQq}{2��R}$���������� | B�� | ��СΪ$\frac{kdQq}{��{R}^{2}}$���������� | ||
| C�� | ��СΪ$\frac{kdQq}{��{R}^{3}}$���������� | D�� | ��СΪ$\frac{kdQq}{2��{R}^{3}}$���������� |
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com