

分析 (1)只有保证小球沿水平方向抛出才能保证物体做平抛运动.
(2)根据平抛运动的规律可求得物体平抛运动的速度.
(3)根据动能定理,结合平抛运动的规律以及数学知识求出s的大小,结合图象求出h的大小.
(4)根据竖直方向上连续相等时间内的位移之差是一恒量求出相等的时间间隔,结合水平位移和时间间隔求出初速度.
解答 解:(1)由于在烧断细线前小球做圆周运动,故速度方向沿切线方向,所以只有在悬点正下方物体的速度沿水平方向,要小球做平抛运动,则小球平抛的初速度只能沿水平方向,故只有保证小球沿水平方向抛出才能保证物体做平抛运动.
(2)由于小球做平抛运动故有在水平方向有s=vt,
在竖直方向有h-L=$\frac{1}{2}g{t}^{2}$,
故有:${v}_{0}=s\sqrt{\frac{g}{2(h-L)}}$.
(3)释放小球时悬线与竖直方向的夹角θ时,小球平抛的速度v,则有mg(L-Lcosθ)=$\frac{1}{2}m{v}^{2}$…②
则物体在水平方向的位移s=vt…③
联立①②③可得
s2=4(h-L)L(1-cosθ)
显然当cosθ=0时,即有2=4(h-L)L(1-cosθ)
当θ=30°时,cosθ=$\frac{\sqrt{3}}{2}$,s2=4(h-L)L(1-$\frac{\sqrt{3}}{2}$),
故有$\frac{2}{{s}^{2}}=\frac{1}{1-\frac{\sqrt{3}}{2}}=\frac{2}{2-\sqrt{3}}$,则s=$\sqrt{2-\sqrt{3}}$=0.52m.
s2=4(h-L)L(1-cosθ)
故当l=1.0m时有:2=4(h-1)×1,
即h-1=0.5
h=1.5m.
(4)在竖直方向上,根据△y=L=gT2得,T=$\sqrt{\frac{L}{g}}$,则初速度${v}_{0}=\frac{2L}{T}=2\sqrt{gL}$,代入数据解得${v}_{0}=2\sqrt{10×1.25×1{0}^{-2}}$m/s=0.7m/s.
故答案为:(1)以保证小球速度水平(或保证小球做平抛运动),(2)$s\sqrt{\frac{g}{2(h-L)}}$,(3)0.52,1.5.
(4)$2\sqrt{gL}$,0.7m/s
点评 解决本题的关键知道实验的原理以及注意事项,知道平抛运动在水平方向和竖直方向上的运动规律,结合运动学公式和推论灵活求解.


科目:高中物理 来源: 题型:多选题
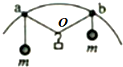 如图,两个轻环a和b套在位于竖直面内的一段固定圆弧上:一细线穿过两轻环,其两端各系一质量为m的小球.在a和b之间的细线上悬挂一小物块.平衡时,a、b间的距离恰好等于圆弧的半径,标记小物块在绳上的位置为O位置.不计所有摩擦,下列说法正确的是( )
如图,两个轻环a和b套在位于竖直面内的一段固定圆弧上:一细线穿过两轻环,其两端各系一质量为m的小球.在a和b之间的细线上悬挂一小物块.平衡时,a、b间的距离恰好等于圆弧的半径,标记小物块在绳上的位置为O位置.不计所有摩擦,下列说法正确的是( )| A. | 细绳aO段与竖直方向的夹角为60° | B. | 细绳aO段与竖直方向的夹角为30° | ||
| C. | 小物块的质量为m | D. | 小物块的质量为2m |
查看答案和解析>>
科目:高中物理 来源: 题型:计算题
查看答案和解析>>
科目:高中物理 来源: 题型:选择题
| A. | E=$\frac{F}{q}$中的场强E是电荷q产生的 | B. | E=$\frac{F}{q}$中的场强E的方向和F方向相同 | ||
| C. | 由E=$\frac{F}{q}$可知E与F成正比,与q成反比 | D. | E=$\frac{kQ}{{r}^{2}}$中的场强E是电荷Q产生的 |
查看答案和解析>>
科目:高中物理 来源: 题型:多选题
| A. | 光的偏振现象说明了光是一种横波 | |
| B. | 做单缝衍射实验时,单缝宽度变窄,衍射条纹间距变宽 | |
| C. | 医学上用激光来切除肿瘤是应用激光的平行度好的特点 | |
| D. | 增透膜主要应用了光的干涉原理 |
查看答案和解析>>
科目:高中物理 来源: 题型:实验题
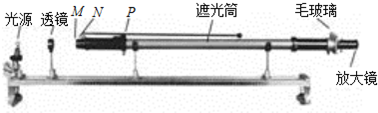
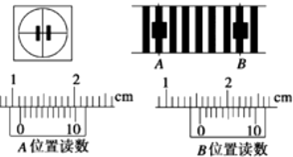
查看答案和解析>>
科目:高中物理 来源: 题型:选择题
| A. | 能到达正对岸 | |
| B. | 渡河的最短时间为30s | |
| C. | 以最短位移渡河时,位移大小为150m | |
| D. | 以最短位移渡河时,位移大小为200m |
查看答案和解析>>
科目:高中物理 来源: 题型:选择题
| A. | ①②③④ | B. | ③④①② | C. | ③④②① | D. | ④①③② |
查看答案和解析>>
科目:高中物理 来源: 题型:计算题
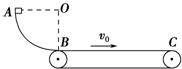 如图所示,一质量为m=2kg的滑块从半径为R=0.2m的光滑四分之一圆弧轨道的顶端A处由静止滑下,A点和圆弧对应的圆心O点等高,圆弧的底端B与水平传送带平滑相接.已知传送带匀速运行的速度为v0=4m/s,B点到传送带右端C点的距离为L=2m.当滑块滑到传送带的右端C时,其速度恰好与传送带的速度相同.(g=10m/s2),求:
如图所示,一质量为m=2kg的滑块从半径为R=0.2m的光滑四分之一圆弧轨道的顶端A处由静止滑下,A点和圆弧对应的圆心O点等高,圆弧的底端B与水平传送带平滑相接.已知传送带匀速运行的速度为v0=4m/s,B点到传送带右端C点的距离为L=2m.当滑块滑到传送带的右端C时,其速度恰好与传送带的速度相同.(g=10m/s2),求:查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com