某人骑自行车以4m/s的速度匀速前进,某时刻在其前面7m处以10m/s速度同向运行的汽车开始关闭发动机,以大小为2m/s2的加速度匀减速行驶,求:
(1)此人在追上汽车之前何时距汽车最远?最大距离为多少?
(2)此人需要多长时间才能追上汽车?此时汽车的速度是多大?
解:(1)当两者速度相等时相距最远
有:v
1=v
2-at
解得t=

此时自行车的位移x
1=v
1t=12m
汽车的位移
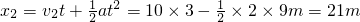
S
m=x
2+7-x
1=16m.
(2)设经过t时间自行车追上汽车,有:

即4t=10t-t
2+7
解得t=7s.
汽车到停止所需的时间

,知自行车追上汽车前,汽车已停止.
汽车的位移

自行车追上汽车所需的位移x″=x′+7m=32m
t″=

此时汽车的速度为零.
答:(1)经过3s两车相距最远,最远距离为16m.
(2)自行车需经过8s追上汽车,此时汽车的速度为零.
分析:(1)两车在速度相等前,距离越来越大,速度相等后,距离越来越小,知速度相等时,距离最远.求出两车速度相等时所需的时间,从而求出两车的位移,根据位移关系求出最大距离.
(2)根据两车的位移关系求出自行车追上汽车的时间,再根据速度公式求出汽车的速度.注意汽车速度为零后不再运动.
点评:该车为运动学中的追及问题,知道两车速度相等时,相距最远.以及知道两车相遇时,位移存在一定的关系.注意汽车减速到零,不再运动.


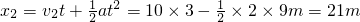

 ,知自行车追上汽车前,汽车已停止.
,知自行车追上汽车前,汽车已停止.


