
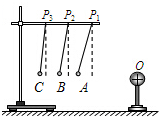
 ��ͼ��ʾ��O��һ������������壬����ϵ��˿���ϵĴ�����С���Ⱥ���ں���ϵ�P1��P2��P3��λ�ã�A��B��C��С�����յ�ƽ��λ�ã��Ƚ�С���ڲ�ͬλ�����ܴ�������������Ĵ�С��������Ĵ�С����ͨ��˿��ƫ����ֱ����ĽǶ���ʾ����������˵����ȷ���ǣ�������
��ͼ��ʾ��O��һ������������壬����ϵ��˿���ϵĴ�����С���Ⱥ���ں���ϵ�P1��P2��P3��λ�ã�A��B��C��С�����յ�ƽ��λ�ã��Ƚ�С���ڲ�ͬλ�����ܴ�������������Ĵ�С��������Ĵ�С����ͨ��˿��ƫ����ֱ����ĽǶ���ʾ����������˵����ȷ���ǣ�������| A�� | A��B��C������ͬһˮƽ���� | B�� | A���ij�ǿ����C���ij�ǿ | ||
| C�� | A���ĵ��Ƶ���C���ĵ��� | D�� | A���ĵ���С��C���ĵ��� |
���� ���ݿ��ض��ɹ�ʽ�ж�������С��֮���������F��ʲô�����йأ�˿��ƫ����ֱ����ĽǶȦ�Խ����������Խ���ݵ��ɵij�ǿ��ʽ$E=k\frac{Q}{{r}^{2}}$��������A��ij�ǿ����C��ij�ǿ��
��� �⣺A��������ͼ��С����A��B��C����ʱ��˿��ƫ����ֱ����ĽǶȲ�ͬ��A��B��C���㲻��ͬһˮƽ���ϣ���ѡ��A����
B�����ݵ��ɵij�ǿ��ʽ$E=k\frac{Q}{{r}^{2}}$��������A��ij�ǿ����C��ij�ǿ����ѡ��B��ȷ��
C�����ɵĵ糡�ߴӵ�����ָ�����ܣ����ŵ糡�߷���������ͣ��ɿ���ABC�ĵ�����С��ѡ��C��D������
��ѡ��B
���� �������Ĺؼ����տ��ض��ɵĹ�ʽ�����ɳ�ǿ��ʽ���Ѷ��еȣ�



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ���������� ��Դ�� ���ͣ���ѡ��
| A�� | ���ݶ���ʽB=$\frac{F}{IL}$���ų���ij��ĴŸ�Ӧǿ��B��F�����ȣ���IL�ɷ��� | |
| B�� | �Ÿ�Ӧǿ��B��ʸ����������������ܰ������ķ�����ͬ | |
| C�� | �Ÿ������Ǵ�N��ָ��S�� | |
| D�� | ��ͨ��������֮�֣�������ʸ�� |
�鿴�𰸺ͽ���>>
��Ŀ���������� ��Դ�� ���ͣ�ѡ����
| A�� | ��˹���ܷ����ڷ����ˡ���Ÿ�Ӧ����������ͨ��ʵ�鷢���ˡ������Ĵ�ЧӦ�� | |
| B�� | �����������ֶ����ж�ͨ�絼������ų��ķ��� | |
| C�� | �ڴų��е��˶����һ���ܵ��������������ã��������������˶����һ�������� | |
| D�� | ��B=$\frac{��}{S}$��֪���Ÿ�Ӧǿ�ȵ��ڴ�����λ����Ĵ�ͨ�������ԴŸ�Ӧǿ��Ҳ�ɽ�����ͨ�ܶ� |
�鿴�𰸺ͽ���>>
��Ŀ���������� ��Դ�� ���ͣ�ѡ����
| A�� | C���� | B�� | C�������� | ||
| C�� | C�������� | D�� | ������������ |
�鿴�𰸺ͽ���>>
��Ŀ���������� ��Դ�� ���ͣ������
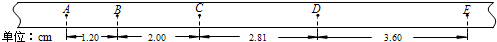
�鿴�𰸺ͽ���>>
��Ŀ���������� ��Դ�� ���ͣ������
 ʵ���ұ�������������
ʵ���ұ��������������鿴�𰸺ͽ���>>
��Ŀ���������� ��Դ�� ���ͣ���ѡ��
| A�� | 1��ͭԭ�ӵ�����Ϊ$\frac{��}{{N}_{A}}$ | B�� | 1��ͭԭ��ռ�е����Ϊ$\frac{M}{{N}_{A}}$ | ||
| C�� | 1m3ͭ����ԭ�ӵ���ĿΪ$\frac{��{N}_{A}}{M}$ | D�� | 1kgͭ����ԭ�ӵ���ĿΪ$\frac{{N}_{A}}{M}$ |
�鿴�𰸺ͽ���>>
��Ŀ���������� ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ���������� ��Դ�� ���ͣ�ѡ����
 ��ͼΪ���ٶ�Ϊv0��ֱ���˶��������v-tͼ����ĩ�ٶ�Ϊvt����ʱ��t�ڣ������ƽ���ٶ�$\overline v$Ϊ��������
��ͼΪ���ٶ�Ϊv0��ֱ���˶��������v-tͼ����ĩ�ٶ�Ϊvt����ʱ��t�ڣ������ƽ���ٶ�$\overline v$Ϊ��������| A�� | $\overline v$��$\frac{1}{2}$��v0+vt�� | B�� | $\overline v$=$\frac{1}{2}$��v0+vt�� | C�� | $\overline v$��$\frac{1}{2}$��v0+vt�� | D�� | ��ȷ�� |
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com