
 “天宫二号”和“神州十一号”交会对接成功,标志着我国在对接技术上迈出了重要一步,用P代表“神州十一号”,Q代表“天宫二号”,它们对接前做圆周运动的情形如图所示,运行方向均为顺时针转动.已知地球质量为M,地球半径为R,引力常量为G,对接前“神舟十一号”离地表的高度为h,则( )
“天宫二号”和“神州十一号”交会对接成功,标志着我国在对接技术上迈出了重要一步,用P代表“神州十一号”,Q代表“天宫二号”,它们对接前做圆周运动的情形如图所示,运行方向均为顺时针转动.已知地球质量为M,地球半径为R,引力常量为G,对接前“神舟十一号”离地表的高度为h,则( )| A. | P的运行速度为$\sqrt{G\frac{M}{R}}$ | B. | Q的向心加速度大于G$\frac{M}{(R+h)^{2}}$ | ||
| C. | P的运行周期大于Q的运行周期 | D. | P适度加速可与Q对接 |
分析 根据万有引力定律和牛顿第二定律有$G\frac{Mm}{{r}_{\;}^{2}}=ma=m\frac{{v}_{\;}^{2}}{r}=m{ω}_{\;}^{2}r=m\frac{4{π}_{\;}^{2}}{{T}_{\;}^{2}}r$,分别解出线速度、加速度和周期与轨道半径的大小关系,根据P和Q的轨道半径大小判断线速度、角速度和周期的大小.P适度加速将做离心运动,可运行至较高的轨道与Q对接.
解答 解:A、根据万有引力提供向心力,有$G\frac{Mm}{(R+h)_{\;}^{2}}=m\frac{{v}_{\;}^{2}}{R+h}$,得P的运行速度$v=\sqrt{\frac{GM}{R+h}}$,故A错误;
B、P的轨道半径等于R+h,根据万有引力提供向心力,有$G\frac{Mm}{(R+h)_{\;}^{2}}=ma$,得$a=\frac{GM}{(R+h)_{\;}^{2}}$,因Q的轨道半径大于R+h,所以向心加速度小于$G\frac{M}{(R+h)_{\;}^{2}}$,故B错误;
C、根据万有引力提供向心力,有$G\frac{Mm}{{r}_{\;}^{2}}=m\frac{4{π}_{\;}^{2}}{{T}_{\;}^{2}}r$,得$T=\sqrt{\frac{4{π}_{\;}^{2}{r}_{\;}^{3}}{GM}}$,轨道半径越小,周期越小,所以P的运行周期小于Q的运行周期,故C错误;
D、P处于低轨道,需加速,使得万有引力不够提供向心力,做离心运动,可能与Q实现对接,故D正确;
故选:D
点评 本题主要考查了万有引力定律、牛顿第二定律、离心运动的应用问题,属于中档题.


 名校课堂系列答案
名校课堂系列答案科目:高中物理 来源: 题型:选择题
| A. | 用紫光照射某种金属发生光电效应,改用绿光照射该金属一定会发生光电效应 | |
| B. | 重核裂变后生成中等质量的核,反应前后质量数守恒,质量守恒 | |
| C. | 将放射性物质放在密闭的铅盒内,可以延长它的半衰期 | |
| D. | 原子核的比结合能越大,原子核越稳定 |
查看答案和解析>>
科目:高中物理 来源: 题型:选择题
| A. | 物体运动的速度为零,加速度不为零 | |
| B. | 物体做直线运动,后一阶段的加速度比前一阶段小,但速度却比前一阶段大 | |
| C. | 当物体所受合力方向与它的速度方向不在同一直线上时,物体一定做曲线运动 | |
| D. | 做匀速圆周运动的物体,速率不变,向心加速度也不变 |
查看答案和解析>>
科目:高中物理 来源: 题型:多选题
| A. | 卫星与碎片碰撞前的线速度大小为$\frac{g{R}^{2}}{r}$ | |
| B. | 卫星与碎片碰撞前运行的周期大小为$\frac{2πr}{R}$$\sqrt{\frac{r}{g}}$ | |
| C. | 卫星与碎片碰撞后运行的周期变大 | |
| D. | 喷气装置对卫星和碎片整体所做的功为$\frac{({n}^{2}-1)({m}_{1}+{m}_{2})g{R}^{2}}{2{n}^{2}r}$ |
查看答案和解析>>
科目:高中物理 来源: 题型:计算题
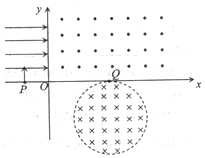 如图所示,在第Ⅱ象限内有水平向右的匀强电场,在第Ⅰ象限和第Ⅳ象限的圆形区域内分别存在如图所示的匀强磁场,在第Ⅳ象限磁感应强度大小是第Ⅰ象限的2倍.圆形区域与x轴相切于Q点,Q到O点的距离为L.有一个带电粒子质量为m,电量为q,以垂直于x轴的初速度从x轴上的P点进入匀强电场中,并且恰好与y轴的正方向成60°角以速度v进入第Ⅰ象限,又恰好垂直于x轴在Q点进入圆形区域磁场,射出圆形区域磁场后与x轴正向成30°角再次进入第Ⅰ象限.不计重力.求:
如图所示,在第Ⅱ象限内有水平向右的匀强电场,在第Ⅰ象限和第Ⅳ象限的圆形区域内分别存在如图所示的匀强磁场,在第Ⅳ象限磁感应强度大小是第Ⅰ象限的2倍.圆形区域与x轴相切于Q点,Q到O点的距离为L.有一个带电粒子质量为m,电量为q,以垂直于x轴的初速度从x轴上的P点进入匀强电场中,并且恰好与y轴的正方向成60°角以速度v进入第Ⅰ象限,又恰好垂直于x轴在Q点进入圆形区域磁场,射出圆形区域磁场后与x轴正向成30°角再次进入第Ⅰ象限.不计重力.求:查看答案和解析>>
科目:高中物理 来源: 题型:填空题
查看答案和解析>>
科目:高中物理 来源: 题型:选择题
 如图所示,交流电流表与灯泡串联,先后在M、N间加上不同的交变电压,第一次加电压随时间按甲图的正弦规律变化;第二次加电压随时间按乙图规律变化.若甲、乙图中的U0、T所表示的电压、周期值是相同的,则这两次交流电流表读数之比I1:I2为( )
如图所示,交流电流表与灯泡串联,先后在M、N间加上不同的交变电压,第一次加电压随时间按甲图的正弦规律变化;第二次加电压随时间按乙图规律变化.若甲、乙图中的U0、T所表示的电压、周期值是相同的,则这两次交流电流表读数之比I1:I2为( )| A. | 1:$\sqrt{5}$ | B. | $\sqrt{5}$:1 | C. | $\sqrt{5}$:$\sqrt{2}$ | D. | 1:2 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com