
分析 (1)根据库仑引力提供向心力得出电子的动能,结合玻尔的量子化条件求出轨道半径rn的表达式;结合氢原子的能级能量等于动能和势能之和求出En的表达式;
(2)根据能级跃迁时,辐射的光子能量等于两能级间的能级差,结合能量的表达式求出光子的频率的表达式;
通过频率等于周期的倒数,结合圆周运动的知识,根据数学极限思维得出频率的表达式,从而进行证明.
解答 解:(1)①对于氢原子,库仑力提供电子绕核运动的向心力,根据牛顿运动定律得
$k\frac{{e}^{2}}{{r}^{2}}=m\frac{{v}^{2}}{r}$,
根据玻尔的量子化条件
mvnrn=n$\frac{h}{2π}$,n=1,2,3…,
联立以上两式解得${v}_{n}=\frac{2πk{e}^{2}}{nh}$,${r}_{n}=\frac{m{h}^{2}}{4{π}^{2}{m}^{2}k{e}^{2}}{n}^{2}$,n=1,2,3…
②选取无穷远处为零势能面,则得
${E}_{n}=\frac{1}{2}m{{v}_{n}}^{2}-k\frac{{e}^{2}}{{r}_{n}}$,
将vn、rn的表达式代入,整理得
${E}_{n}=-\frac{2{π}^{2}m{k}^{2}{e}^{4}}{{n}^{2}{h}^{2}}$,n=1,2,3…
(2)①根据玻尔理论,当原子从较高能量状态En+1向较低能量状态En跃迁时,发射一个光子,其频率为
hγn=En+1-En,
所以${γ}_{n}=\frac{{E}_{n+1}-{E}_{n}}{h}$,
将En+1、En的表达式代入,整理得${γ}_{n}=\frac{2{π}^{2}m{k}^{2}{e}^{4}(2n+1)}{{h}^{3}{n}^{2}(n+1)^{2}}$.
②根据以上表达式,当n→∞时,2n+1→2n,n+1→n,γn的表达式为
${γ}_{n}=\frac{4{π}^{2}m{k}^{2}{e}^{4}}{{h}^{3}{n}^{3}}$
电子在第n轨道上的转动频率为
${f}_{n}=\frac{1}{{T}_{n}}=\frac{1}{\frac{2π{r}_{n}}{{v}_{n}}}=\frac{{v}_{n}}{2π{r}_{n}}$,
将rn的表达式代入,整理得
${f}_{n}=\frac{4{π}^{2}{k}^{2}m{e}^{4}}{{h}^{3}}•\frac{1}{{n}^{3}}={γ}_{n}$.
答:(1)①氢原子的第n(n=1,2,3…)轨道半径rn的表达式为${r}_{n}=\frac{m{h}^{2}}{4{π}^{2}{m}^{2}k{e}^{2}}{n}^{2}$,n=1,2,3…;
②氢原子的第n(n=1,2,3…)能级En的表达式为${E}_{n}=-\frac{2{π}^{2}m{k}^{2}{e}^{4}}{{n}^{2}{h}^{2}}$,n=1,2,3….
(2)①电子从n+1轨道跃迁到n轨道放出的光子的频率γn的表达式为${γ}_{n}=\frac{4{π}^{2}m{k}^{2}{e}^{4}}{{h}^{3}{n}^{3}}$,n=1,2,3…;
②证明如上所示.
点评 解决本题的关键能够正确地建立物理模型,选择合适的规律进行求解,知道原子的能量等于电子的动能和原子势能之和,知道能级跃迁时,辐射的光子能量等于两能级间的能级差.


 黄冈小状元解决问题天天练系列答案
黄冈小状元解决问题天天练系列答案 三点一测快乐周计划系列答案
三点一测快乐周计划系列答案科目:高中物理 来源: 题型:多选题
| A. | 同步卫星处于平衡状态 | |
| B. | 同步卫星角速度与地球自转角速度相等 | |
| C. | 同步卫星的高度是一定的 | |
| D. | 线速度应大于第一宇宙速度 |
查看答案和解析>>
科目:高中物理 来源: 题型:选择题
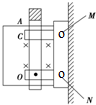 如图所示为一种自动跳闸的闸刀开关示意图,O是转动轴,A是绝缘手柄,C是闸刀卡口,M、N接电源线.闸刀处于垂直纸面向里B=0.1T的匀强磁场中,CO间距离10cm.当磁场力为0.2N时,闸刀开关会自动跳开.则要使闸刀开关能跳开,通过闸刀CO中的电流的大小和方向为( )
如图所示为一种自动跳闸的闸刀开关示意图,O是转动轴,A是绝缘手柄,C是闸刀卡口,M、N接电源线.闸刀处于垂直纸面向里B=0.1T的匀强磁场中,CO间距离10cm.当磁场力为0.2N时,闸刀开关会自动跳开.则要使闸刀开关能跳开,通过闸刀CO中的电流的大小和方向为( )| A. | 电流大小为2A,电流方向O→C | B. | 电流大小为2A,电流方向C→O | ||
| C. | 电流大小为20A,电流方向O→C | D. | 电流大小为20A,电流方向C→O |
查看答案和解析>>
科目:高中物理 来源: 题型:填空题
查看答案和解析>>
科目:高中物理 来源: 题型:多选题
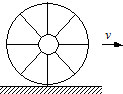 如图所示,电视画面每隔t=$\frac{1}{30}$秒更迭一帧.当屏幕上出现一辆车匀速行驶的情景时,观众如果注视车辆的辐条,往往会产生奇怪的感觉,设车轮上有八根对称分布完全相同的辐条,下列说法中错误的是( )
如图所示,电视画面每隔t=$\frac{1}{30}$秒更迭一帧.当屏幕上出现一辆车匀速行驶的情景时,观众如果注视车辆的辐条,往往会产生奇怪的感觉,设车轮上有八根对称分布完全相同的辐条,下列说法中错误的是( )| A. | 若车轮转速为3.75r/s,则观众觉得车轮是不动的 | |
| B. | 若车轮转速为30r/s,则观众觉得车轮是倒转的 | |
| C. | 若车轮转速为31r/s,则观众觉得车轮是倒转的 | |
| D. | 若车轮转速为29r/s,则观众觉得车轮是倒转的 |
查看答案和解析>>
科目:高中物理 来源: 题型:选择题

| A. | 质点在15s前、后的速度方向相反 | |
| B. | 质点匀加速运动的加速度的大小与匀减速运动加速度的大小之比为4:1 | |
| C. | 质点15s末离出发点最远,20秒末回到出发点 | |
| D. | 质点在前10s内的平均速率为9m/s |
查看答案和解析>>
科目:高中物理 来源: 题型:多选题
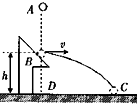 如图所示,从A点由静止释放一弹性小球,一段时间后与固定斜面上B点发生碰撞,碰后小球速度大小不变,方向变为水平方向,又经过相同的时间落于地面上C点,已知地面上D点位于B点正下方,B、D间的距离为h,则( )
如图所示,从A点由静止释放一弹性小球,一段时间后与固定斜面上B点发生碰撞,碰后小球速度大小不变,方向变为水平方向,又经过相同的时间落于地面上C点,已知地面上D点位于B点正下方,B、D间的距离为h,则( )| A. | A、B两点间的距离为$\frac{h}{2}$ | B. | A、B两点间的距离为h | ||
| C. | C、D两点间的距离为2h | D. | C、D两点间的距离为$\frac{2\sqrt{3}}{3}$h |
查看答案和解析>>
科目:高中物理 来源: 题型:选择题
| A. | 做曲线运动的物体加速度可以为零 | |
| B. | 做匀速圆周运动的物体所受合外力大小、方向都保持不变 | |
| C. | 做圆周运动的物体所受合外力突然消失,物体一定沿圆周的半径方向飞出 | |
| D. | 飞机在空中沿半径为R的水平圆周盘旋时,飞机机翼一定处于倾斜状态 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com