
 如图所示,A、B为水平传送带的两个端点,C、D为倾斜传送带的两个端点,B,C之间平滑连接.长度不计,两传送带均沿顺时针方向运行,速率分别为v1=10m/s,v2=5m/s.倾斜传送带与水平面的夹角θ=30°,在水平传送带A点处轻放一质量m=2kg的小物块,小物块速度能达到v1并先后经过B点、C点,最后刚好能到达D点(不计从B到C之间的能量损失),小物块与传送带间的动摩擦因数均为μ=$\frac{\sqrt{3}}{6}$,g取10m/s2.求:
如图所示,A、B为水平传送带的两个端点,C、D为倾斜传送带的两个端点,B,C之间平滑连接.长度不计,两传送带均沿顺时针方向运行,速率分别为v1=10m/s,v2=5m/s.倾斜传送带与水平面的夹角θ=30°,在水平传送带A点处轻放一质量m=2kg的小物块,小物块速度能达到v1并先后经过B点、C点,最后刚好能到达D点(不计从B到C之间的能量损失),小物块与传送带间的动摩擦因数均为μ=$\frac{\sqrt{3}}{6}$,g取10m/s2.求:分析 (1)根据动能定理求解AB的最短位移;
(2)分析物体在CD段的运动情况,根据牛顿第二定律求解加速度大小,再根据位移速度关系求解CD的长度;
(3)利用速度时间关系分别求出AB段、CD段的运动时间即可;
(4)分别计算出物块速度从v1减小到v2过程中、速度从v2减小到0的过程中皮带的位移,再计算出物块相对于皮带的位移,然后求和即可.
解答 解:(1)小物块从A到B根据动能定理可得:μmgL1=$\frac{1}{2}m{v}_{1}^{2}$,
解得:L1=$10\sqrt{3}m$;
(2)小物块刚好到倾斜传送带上至两者共速前,受到沿斜面向下的滑动摩擦力作用,做匀减速直线运动,在速度减速到v2过程中,根据牛顿第二定律可得物块的加速度大小为a1=gsinθ+μgcosθ=10×0.5+$\frac{\sqrt{3}}{6}×10×\frac{\sqrt{3}}{2}$=7.5m/s2,
根据匀变速直线运动位移速度关系可得:${v}_{1}^{2}-{v}_{2}^{2}=2{a}_{1}{x}_{1}$,
解得x1=5m;
小物块达到与传送带速度相等后继续减速运动,速度减速到零的过程中,摩擦力方向沿斜面向上,
根据牛顿第二定律可得加速度a2=gsinθ-μgcosθ=10×0.5-$\frac{\sqrt{3}}{6}×10×\frac{\sqrt{3}}{2}$=2.5m/s2,
根据${v}_{2}^{2}-0=2{a}_{2}{x}_{2}$可得减速到零的位移为:x2=5m;
则L2=x1+x2=5m+5m=10m;
(3)物块在AB上运动时的时间为t1,则:t1=$\frac{{v}_{1}-0}{μg}=\frac{10-0}{\frac{\sqrt{3}}{6}×10}=2\sqrt{3}s$,
设在CD上运动时,前一段时间为t2,后一段时间为t3,则:
由v2=v1-a1t2,解得t2=$\frac{2}{3}s$,
由0=v2-a2t3得t3=2s;
所以运动的总时间为:t=t1+t2+t3=$(2\sqrt{3}+\frac{8}{3})s$;
(4)物块速度减速到v2过程中,倾斜传送带的位移x3=v2t2=5×$\frac{2}{3}m=\frac{10}{3}m$,
此过程中小物块相对于传送带的位移△s1=x1-x3=5-$\frac{10}{3}=\frac{5}{3}m$,
物块速度从v2减速到零时间内倾斜传送带的位移为:x4=v2t3=5×2m=10m,
此过程中小物块相对于传送带的位移△s2=x4-x2=10-5=5m,
所以小物块相对于传送带的位移为△s=△s1+△s2=$\frac{5}{3}+5=\frac{20}{3}m$.
答:(1)AB之间的距离L1至少为$10\sqrt{3}m$;
(2)CD之间的距离为10m;
(3)AB之间的距离取最小值时小物块从A运动到D的总时间为$(2\sqrt{3}+\frac{8}{3})s$;
(4)小物块在倾斜传送带上运动的过程中相对倾斜传送带滑动的距离为$\frac{20}{3}$m.
点评 解答本题的关键是弄清楚物块的受力情况和运动情况;对于牛顿第二定律的综合应用问题,关键是弄清楚物体的运动过程和受力情况,利用牛顿第二定律或运动学的计算公式求解加速度,再根据题目要求进行解答;知道加速度是联系静力学和运动学的桥梁.


 长江作业本同步练习册系列答案
长江作业本同步练习册系列答案 小天才课时作业系列答案
小天才课时作业系列答案 一课四练系列答案
一课四练系列答案科目:高中物理 来源: 题型:选择题
| A. | 正电荷放于电势越低处,电势能越小 | |
| B. | 负电荷放于电场线越密处,电势能越小 | |
| C. | 正电荷由电势低处移到电势高处,电场力作正功 | |
| D. | 负电荷沿电场线移动,电势能减小 |
查看答案和解析>>
科目:高中物理 来源: 题型:选择题

| A. | 这列波的周期为2.0s | |
| B. | 这列波的振幅为10cm | |
| C. | 此时刻质点P的振动方向沿y轴正方向 | |
| D. | 此时刻质点Q的加速度为零 |
查看答案和解析>>
科目:高中物理 来源: 题型:计算题

查看答案和解析>>
科目:高中物理 来源: 题型:填空题
 在学到自由落体这一部分内容后,有同学计算,若有雨滴从距地面2.5km高空自由落下,到达地面时速度将达到700m/s.这雨滴无异于一发高速运动的子弹.事实上谁也未见过如此高速的雨滴,这引发了一些同学的思考:雨滴在下落时肯定受到了空气阻力的作用.哪它究竟是如何运动的呢?有一组同学设计了一个实验,用胶木球在水中的自由下落来模拟雨滴在空气中的下落过程.实验中,胶木球从某一高度竖直落下,用闪光照相方法拍摄了小球在不同时刻的位置,如图所示.
在学到自由落体这一部分内容后,有同学计算,若有雨滴从距地面2.5km高空自由落下,到达地面时速度将达到700m/s.这雨滴无异于一发高速运动的子弹.事实上谁也未见过如此高速的雨滴,这引发了一些同学的思考:雨滴在下落时肯定受到了空气阻力的作用.哪它究竟是如何运动的呢?有一组同学设计了一个实验,用胶木球在水中的自由下落来模拟雨滴在空气中的下落过程.实验中,胶木球从某一高度竖直落下,用闪光照相方法拍摄了小球在不同时刻的位置,如图所示.查看答案和解析>>
科目:高中物理 来源: 题型:计算题
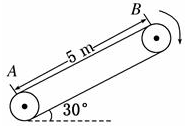 如图所示,传送带与水平面之间的夹角为θ=30°,其上A、B两点间的距离为L=5m,传送带在电动机的带动下以v=1m/s的速度匀速运动,质量为m=10kg的小物体(可视为质点)与传送带之间的动摩擦因数μ=$\frac{{\sqrt{3}}}{2}$,(g取10m/s2 ),求:
如图所示,传送带与水平面之间的夹角为θ=30°,其上A、B两点间的距离为L=5m,传送带在电动机的带动下以v=1m/s的速度匀速运动,质量为m=10kg的小物体(可视为质点)与传送带之间的动摩擦因数μ=$\frac{{\sqrt{3}}}{2}$,(g取10m/s2 ),求:查看答案和解析>>
科目:高中物理 来源: 题型:多选题
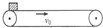 如图所示,足够长的水平传送带以v0=2m/s的速度匀速运行,t=0时,在最左端轻放一个小滑块,t=2s时,传送带突然制动停下,已知滑块与传送带之间的滑动摩擦因数为μ=0.2,g=10m/s2,在下图中,关于滑块相对地面运动的v-t图象不正确的是( )
如图所示,足够长的水平传送带以v0=2m/s的速度匀速运行,t=0时,在最左端轻放一个小滑块,t=2s时,传送带突然制动停下,已知滑块与传送带之间的滑动摩擦因数为μ=0.2,g=10m/s2,在下图中,关于滑块相对地面运动的v-t图象不正确的是( )| A. |  | B. |  | C. |  | D. |  |
查看答案和解析>>
科目:高中物理 来源: 题型:计算题
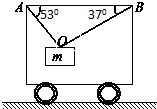 如图所示,质量为m的物体被两根细绳OA、OB挂在小车上,两根细绳与车顶水平面夹角分别为530和370.已知sin37°=0.6,cos37°=0.8,求:
如图所示,质量为m的物体被两根细绳OA、OB挂在小车上,两根细绳与车顶水平面夹角分别为530和370.已知sin37°=0.6,cos37°=0.8,求:查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com