
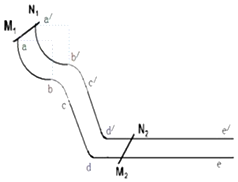
 如图所示,竖直放置的平行导轨由四部分组成,其中只有水平部分是导体材料做的,其余部分均为绝缘材料,整个轨道处在竖直向上的匀强磁场中(磁场未画出).ab、a'b'是四分之一光滑圆弧形轨道,下端切线水平;bc、b'c'是抛物线轨道,cd、c'd'是倾斜轨道,de、d'e'是光滑水平轨道(足够长).倾斜轨道与水平轨道平滑连接.金属棒过dd'前后的速度大小不变,金属杆M1N1从静止开始沿轨道顶端aa'下滑,与抛物线轨道恰好无相互作用力并且恰好沿着倾斜轨道匀速滑下,之后进入水平轨道(0水平轨道上原来放有一根金属杆M2N2),在运动过程中两杆始终与导轨垂直并接触良好.已知圆弧半径为R=0.2m,M1N1的质量为m=1kg,M2N2的质量为2m,cd、c'd'倾斜轨道倾角θ=53°(sin53°=0.8,cos53°=0.6),cd、c'd'倾斜轨道长度s=0.5m,取重力加速度大小g=10m/s2.求:
如图所示,竖直放置的平行导轨由四部分组成,其中只有水平部分是导体材料做的,其余部分均为绝缘材料,整个轨道处在竖直向上的匀强磁场中(磁场未画出).ab、a'b'是四分之一光滑圆弧形轨道,下端切线水平;bc、b'c'是抛物线轨道,cd、c'd'是倾斜轨道,de、d'e'是光滑水平轨道(足够长).倾斜轨道与水平轨道平滑连接.金属棒过dd'前后的速度大小不变,金属杆M1N1从静止开始沿轨道顶端aa'下滑,与抛物线轨道恰好无相互作用力并且恰好沿着倾斜轨道匀速滑下,之后进入水平轨道(0水平轨道上原来放有一根金属杆M2N2),在运动过程中两杆始终与导轨垂直并接触良好.已知圆弧半径为R=0.2m,M1N1的质量为m=1kg,M2N2的质量为2m,cd、c'd'倾斜轨道倾角θ=53°(sin53°=0.8,cos53°=0.6),cd、c'd'倾斜轨道长度s=0.5m,取重力加速度大小g=10m/s2.求:分析 (1)棒M1N1在ab之间运动的过程中机械能守恒,由此求出到达b的速度;然后将运动分解即可求出;
(2)将c点的速度分解,即可求出棒M1N1到达c的速度;由动量守恒即可求出棒M1N1最终的速度;
(3)整个过程中损失的机械能为摩擦产生的内能以及电磁感应的过程中产生的内能,由此即可求出.
解答 解:(1)棒M1N1在ab之间运动的过程中机械能守恒,得:$mgR=\frac{1}{2}mv_0^2$ ①,
解得${v}_{0}=\sqrt{2gR}=\sqrt{2×10×0.2}=2m/s$ ②,
设棒M1N1平抛运动的时间为t1,则竖直方向:vy=gt1 ③
根据题意,在c点:vy=v0tanθ ④
由②③④,代入数据得:t1=$\frac{4}{15}$s ⑤
(2)棒M1N1到达c的速度:${v}_{1}=\frac{{v}_{0}}{cosθ}=\frac{2}{\frac{3}{5}}=\frac{10}{3}m/s$ ⑥,
金属棒M1N1进入水平轨道后,由于轨道是金属导轨,两个金属棒与轨道组成闭合回路,在电路中产生感应电动势,金属棒M1N1和M2N2的ab系统水平方向的动量守恒,设向右为正方向,有:
mv1=(m+2m)v2 ⑦,
由②⑥⑦解得:${v}_{2}=\frac{1}{3}{v}_{1}=\frac{10}{9}m/s$
(3)金属棒M1N1在斜面上运动的过程中,摩擦生热:Q1=μmgs0cosθ ⑧
由于做匀速直线运动,则:μmgcosθ=mgsinθ ⑨
联立得Q1=mgs0sinθ
代入数据得:Q1=4.0J
金属棒M1N1和M2N2相互作用的过程中产生的电热:${Q}_{2}=\frac{1}{2}m{v}_{1}^{2}-\frac{1}{2}(m+2m){v}_{2}^{2}$,
代入数据得:Q2=3.7J
所以:E=Q1+Q2=4.0J+3.7J=7.7J
答:(1)金属杆M1N1在bc、b'c'抛物线轨道上运动的时间是$\frac{4}{15}$s;
(2)金属棒M1N1和M2N2的最终速度是$\frac{10}{9}$m/s;
(3)整个过程中损失的机械能△E是7.7J.
点评 该题属于力、电综合,解答该题的思路要注意考虑两点:一是从力的角度,可以根据平抛运动、动量守恒定律,或根据平衡条件、牛顿第二定律列出方程;二是能量,分析涉及电磁感应现象中的能量转化问题,根据动能定理、功能关系等列方程求解.


科目:高中物理 来源: 题型:选择题
| A. | 周期变大 | B. | 速率变大 | C. | 动能变大 | D. | 向心加速度变大 |
查看答案和解析>>
科目:高中物理 来源: 题型:实验题
 某同学想测量某电池的电动势E和内阻r,选用器材如下:
某同学想测量某电池的电动势E和内阻r,选用器材如下:查看答案和解析>>
科目:高中物理 来源: 题型:多选题
 如图所示,虚线EF左侧区域Ⅰ内有垂直纸面向里的匀强磁场,磁感应强度大小为B,右侧区域Ⅱ内有垂直于纸面向外的匀强磁场,磁感应强度大小为2B.边长为L、粗细均匀的正方形金属线框在区域Ⅰ内,线框平面与磁场垂直,cd边与虚线平行,线框的电阻为R,现使线框由图示位置以速度v向右匀速运动,则在线框通过EF的过程中( )
如图所示,虚线EF左侧区域Ⅰ内有垂直纸面向里的匀强磁场,磁感应强度大小为B,右侧区域Ⅱ内有垂直于纸面向外的匀强磁场,磁感应强度大小为2B.边长为L、粗细均匀的正方形金属线框在区域Ⅰ内,线框平面与磁场垂直,cd边与虚线平行,线框的电阻为R,现使线框由图示位置以速度v向右匀速运动,则在线框通过EF的过程中( )| A. | 通过线框截面的电量为$\frac{B{L}^{2}}{R}$ | |
| B. | 线框中电流的大小为$\frac{3BLv}{R}$ | |
| C. | 线框所受的安培力的大小为$\frac{6{B}^{2}{L}^{2}v}{R}$ | |
| D. | 线框中产生的焦耳热为$\frac{9{B}^{2}{L}^{3}v}{R}$ |
查看答案和解析>>
科目:高中物理 来源: 题型:实验题
查看答案和解析>>
科目:高中物理 来源: 题型:多选题
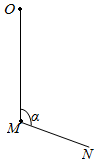 如图,柔软轻绳ON的一端O固定,其中间某点M拴一重物,用手拉住绳的另一端N.初始时,OM竖直且MN被拉直,OM与MN之间的夹角α(α>$\frac{π}{2}$).现将重物向右上方缓慢拉起,并保持夹角α不变,在OM由竖直被拉到水平的过程中( )
如图,柔软轻绳ON的一端O固定,其中间某点M拴一重物,用手拉住绳的另一端N.初始时,OM竖直且MN被拉直,OM与MN之间的夹角α(α>$\frac{π}{2}$).现将重物向右上方缓慢拉起,并保持夹角α不变,在OM由竖直被拉到水平的过程中( )| A. | MN上的张力逐渐增大 | B. | MN上的张力先增大后减小 | ||
| C. | OM上的张力逐渐增大 | D. | OM上的张力先增大后减小 |
查看答案和解析>>
科目:高中物理 来源: 题型:计算题
查看答案和解析>>
科目:高中物理 来源: 题型:实验题

查看答案和解析>>
科目:高中物理 来源: 题型:选择题
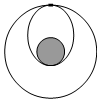 小型登月器连接在航天站上,一起绕月球做圆周运动,其轨道半径为月球半径的5倍,某时刻,航天站使登月器减速分离,登月器沿如图所示的椭圆轨道登月,在月球表面逗留一段时间完成科考工作后,经快速启动仍沿原椭圆轨道返回,当第一次回到分离点时恰与航天站对接,整个过程中航天站保持原轨道绕月运行(登月器减速登月及快速启动过程的时间可以忽略不计).已知月球表面的重力加速度为g,月球半径为R,不考虑月球自转的影响,则登月器可以在月球上停留的最短时间约为( )
小型登月器连接在航天站上,一起绕月球做圆周运动,其轨道半径为月球半径的5倍,某时刻,航天站使登月器减速分离,登月器沿如图所示的椭圆轨道登月,在月球表面逗留一段时间完成科考工作后,经快速启动仍沿原椭圆轨道返回,当第一次回到分离点时恰与航天站对接,整个过程中航天站保持原轨道绕月运行(登月器减速登月及快速启动过程的时间可以忽略不计).已知月球表面的重力加速度为g,月球半径为R,不考虑月球自转的影响,则登月器可以在月球上停留的最短时间约为( )| A. | 10π$\sqrt{\frac{5R}{g}}$-6π$\sqrt{\frac{3R}{g}}$ | B. | 6π$\sqrt{\frac{3R}{g}}$-4$\sqrt{\frac{2R}{g}}$ | C. | 10π$\sqrt{\frac{5R}{g}}$-2π$\sqrt{\frac{R}{g}}$ | D. | 6π$\sqrt{\frac{3R}{g}}$-2π$\sqrt{\frac{R}{g}}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com