
 如图所示,PQCD为光滑的轨道,其中PQ是水平的,CD是竖直平面内的圆轨道,与PQ相切于C点,且半径R=0.5m,圆轨道下端不重叠,物体可从水平轨道右侧运动冲上轨道,并从左侧离开轨道.质量m=0.1kg的A滑块静止在水平轨道上,另一质量M=0.5kg的B滑块前端装有以轻质弹簧(A、B均可视为质点),以速度v0向左运动并与滑块A发生弹性正碰,若相碰后A滑块能过半圆最高点D,取重力加速度g=10m/s2,则:
如图所示,PQCD为光滑的轨道,其中PQ是水平的,CD是竖直平面内的圆轨道,与PQ相切于C点,且半径R=0.5m,圆轨道下端不重叠,物体可从水平轨道右侧运动冲上轨道,并从左侧离开轨道.质量m=0.1kg的A滑块静止在水平轨道上,另一质量M=0.5kg的B滑块前端装有以轻质弹簧(A、B均可视为质点),以速度v0向左运动并与滑块A发生弹性正碰,若相碰后A滑块能过半圆最高点D,取重力加速度g=10m/s2,则:分析 (1)相碰后A滑块能过半圆最高点D,由重力提供向心力,由牛顿第二定律求出滑块A到达轨道最高点D的速度.滑块A从C到D的过程,由机械能守恒求得A与B碰撞后的速度,再对于碰撞过程,根据动量守恒定律与机械能守恒定律可以求出B的初速度.
(2)滑块B与滑块A速度相等时弹簧压缩量最大弹性势能最大,碰撞过程系统动量守恒、机械能守恒,应用动量守恒定律与机械能守恒定律可以求出最大弹性势能.
(3)A滑块冲上圆轨道后不脱离轨道,第一种情况:A在圆心下方$\frac{1}{4}$圆弧上运动.第二种情况:A通过最高点D.根据临界条件和机械能守恒定律求解.
解答 解:(1)设滑块A过D点时速度为vD,B与A碰撞后,B与A的速度分别为v1、v2,B碰撞前的速度为v0
过圆轨道最高点D的临界条件是重力提供向心力,由牛顿第二定律得:mg=m$\frac{{v}_{D}^{2}}{R}$
滑块A从C到D的过程,由机械能守恒定律得:$\frac{1}{2}$mv22=mg•2R+$\frac{1}{2}$mvD2,
B与A发生弹性碰撞,碰撞过程系统的动量守恒、机械能守恒,以向左为正方向,由动量守恒定律得:Mv0=Mv1+mv2,
由机械能守恒定律得:$\frac{1}{2}$Mv02=$\frac{1}{2}$Mv12+$\frac{1}{2}$mv22
离那里并代入数据解得:v0=3m/s;
(2)由于B与A碰撞后,当两者速度相同时有最大弹性势能Ep,设共同速度为v,A、B碰撞过程系统动量守恒、机械能守恒,以向左为正方向,由动量守恒定律得:
Mv0=(M+m)v
由机械能守恒定律得:$\frac{1}{2}$Mv02=EP+$\frac{1}{2}$(M+m)v2,
联立并代入数据解得:Ep=0.375J;
(3)欲使A滑块冲上圆轨道后不脱离轨道,有以下两种情况:
情况一:A到达与圆心等高处,速度为0.
由机械能守恒定律得 mgR=$\frac{1}{2}m{v}_{1}^{2}$
可得 v1=$\sqrt{10}$m/s
情况二:A过最高点,恰好过最高点时,有 $\frac{1}{2}$mv22=mg•2R+$\frac{1}{2}$mvD2,
可得 v2=5m/s
综合以上两种情况可知,A的速度应为:0<v≤$\sqrt{10}$m/s.或v≥5m/s.
答:(1)B滑块的最少速度为3m/s;
(2)如果滑块A恰好能过C点,滑块B与滑块A相碰后轻质弹簧的最大弹性势能为0.375J.
(3)A滑块碰撞后的速度应为:0<v≤$\sqrt{10}$m/s.或v≥5m/s.
点评 本题考查了动量守恒定律和机械能守恒定律的应用,分析清楚物体运动过程是解题的关键,应用牛顿第二定律、动量守恒定律与机械能守恒定律可以解题;知道滑块做圆周运动的临界条件、应用牛顿第二定律求出经过圆形轨道最高点的速度是解题的前提.


科目:高中物理 来源: 题型:多选题
 将一金属小球置于竖直放置的带电平行金属板间,A、B间电场线分布如图所示,则下列判断正确的是( )
将一金属小球置于竖直放置的带电平行金属板间,A、B间电场线分布如图所示,则下列判断正确的是( )| A. | EM>EN,φM>φN | |
| B. | EM<EN,φM>φN | |
| C. | 将正试探电荷从M点移到N点,电场力做正功 | |
| D. | 将负试探电荷从M点移到N点,电荷的电势能减小 |
查看答案和解析>>
科目:高中物理 来源: 题型:多选题

| A. | 根据图乙可知开始计时摆球在C点 | |
| B. | 此单摆的振动频率是0.5Hz | |
| C. | 图中P点向正方向振动 | |
| D. | 根据已知数据可以求得此单摆的摆长为1.0m |
查看答案和解析>>
科目:高中物理 来源: 题型:计算题
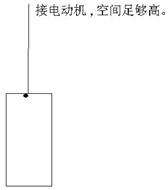 实验用升降机箱体质量为M=55kg,内部天花板到地板间距恰好H=6m.某次实验时,开动电机给升降机箱体恒定的拉力使箱体匀加速上升,加速度大小为$\frac{1}{5}$g,静止启动的同时从天花板处让一弹性小球自由下落.已知小球质量m=5kg,小球和箱体只在竖直方向上运动且每次碰撞都是弹性碰撞,碰撞时间很短,内力远大于外力,忽略空气阻力,g取10m/s2.求:
实验用升降机箱体质量为M=55kg,内部天花板到地板间距恰好H=6m.某次实验时,开动电机给升降机箱体恒定的拉力使箱体匀加速上升,加速度大小为$\frac{1}{5}$g,静止启动的同时从天花板处让一弹性小球自由下落.已知小球质量m=5kg,小球和箱体只在竖直方向上运动且每次碰撞都是弹性碰撞,碰撞时间很短,内力远大于外力,忽略空气阻力,g取10m/s2.求:查看答案和解析>>
科目:高中物理 来源: 题型:多选题
 如图所示,质量相同的甲乙两个小物块,甲从竖直固定的$\frac{1}{4}$光滑圆弧轨道顶端由静止滑下,轨道半径为R,圆弧底端切线水平,乙从高为R的光滑斜面顶端由静止滑下.下列判断正确的是( )
如图所示,质量相同的甲乙两个小物块,甲从竖直固定的$\frac{1}{4}$光滑圆弧轨道顶端由静止滑下,轨道半径为R,圆弧底端切线水平,乙从高为R的光滑斜面顶端由静止滑下.下列判断正确的是( )| A. | 两物块到达底端时动能相同 | |
| B. | 两物块到达底端时速度相同 | |
| C. | 两物块到达底端时,两物块速度的大小相等 | |
| D. | 两物块运动到底端的过程中重力做功相同 |
查看答案和解析>>
科目:高中物理 来源: 题型:选择题
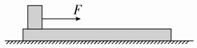 如图所示,在光滑水平面上有一长木板,质量为M,在木板左端放一质量为m的物块,物块与木板间的滑动摩擦力为Ff,给物块一水平向右的恒力F,当物块相对木板滑动L距离时,木板运动位移为x,则下列说法正确的是( )
如图所示,在光滑水平面上有一长木板,质量为M,在木板左端放一质量为m的物块,物块与木板间的滑动摩擦力为Ff,给物块一水平向右的恒力F,当物块相对木板滑动L距离时,木板运动位移为x,则下列说法正确的是( )| A. | 此时物块的动能为FL | B. | 此时物块的动能为(F-Ff)L | ||
| C. | 此时物块的动能为F(L+x)-FfL | D. | 此时木板的动能为Ffx |
查看答案和解析>>
科目:高中物理 来源: 题型:选择题
| A. | 物体动能的增量 | B. | 重力对物体做的功 | ||
| C. | 物体速度的增量 | D. | 重力对物体做功的平均功率 |
查看答案和解析>>
科目:高中物理 来源: 题型:选择题
| A. | 运行速率可按需要取值 | B. | 运动周期可按需要取值 | ||
| C. | 轨道一定在赤道上空 | D. | 离地心的距离可按需要取值 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com