

分析 (1)根据粒子在磁场中的半径的公式可知,粒子的速度越大,半径越大,所以要使电子的侧向位移最大,应让电子从0、2t0、4t0…等时刻进入偏转电场,要使电子的侧向位移最小,应让电子从t0、3t0…等时刻进入偏转电场;
(2)电子垂直打在荧光屏上,根据粒子的运动的轨迹的几何关系,可以求得匀强磁场的磁感应强度的大小;
(3)于各个时刻从偏转电场中出来的电子的速度大小相同,方向也相同,因此电子进入磁场后的半径也相同.根据电子从偏转电场中出来时的最大侧向位移和最小侧向位移可以求得打在荧光屏上的电子束的宽度.
解答 解:(1)由题意可知,要使电子的侧向位移最大,应让电子从0、2t0、4t0…等时刻进入偏转电场,
在这种情况下,电子的侧向位移为
ymax=$\frac{1}{2}a{{t}_{0}}^{2}$+vyt0
ymax=$\frac{1}{2}•\frac{e{U}_{0}}{dm}{{t}_{0}}^{2}+\frac{e{U}_{0}}{dm}{{t}_{0}}^{2}$=$\frac{3e{U}_{0}}{2dm}{{t}_{0}}^{2}$
要使电子的侧向位移最小,应让电子从t0、3t0…等时刻进入偏转电场,
在这种情况下,电子的侧向位移为ymin=$\frac{1}{2}a{{t}_{0}}^{2}$
所以 ymin=$\frac{1}{2}•\frac{e{U}_{0}}{dm}{{t}_{0}}^{2}$
所以最大侧向位移和最小侧向位移之比为ymax:ymin=3:1
(2)设电子从偏转电场中射出时的偏向角为θ,由于电子要垂直打在荧光屏上,
所以电子在磁场中运动半径应为:R=$\frac{l}{sinθ}$
设电子从偏转电场中出来时的速度为vt,垂直偏转极板的速度为vy,
则电子从偏转电场中出来时的偏向角为sinθ=$\frac{{v}_{y}}{{v}_{t}}$
式中vy=$\frac{e{U}_{0}}{dm}$t0
又 R=$\frac{m{v}_{t}}{Be}$
由上述四式可得B=$\frac{{U}_{0}{t}_{0}}{dl}$
(3)由于各个时刻从偏转电场中出来的电子的速度大小相同,方向也相同,
因此电子进入磁场后的半径也相同.
由第(1)问可知电子从偏转电场中出来时的最大侧向位移和最小侧向位移的差值为:
△y=ymax-ymin
所以△y=$\frac{e{U}_{0}}{dm}{{t}_{0}}^{2}$
所以打在荧光屏上的电子束的宽度为△y=$\frac{e{U}_{0}}{dm}{{t}_{0}}^{2}$.
答:(1)电子在刚穿出两板之间时的最大侧向位移与最小侧向位移之比为3:1;
(2)要使侧向位移最大的电子能垂直打在荧光屏上,匀强磁场的磁感应强度为$\frac{{U}_{0}{t}_{0}}{dl}$;
(3)在满足第(2)问的情况下,打在荧光屏上的电子束的宽度为$\frac{e{U}_{0}}{dm}{{t}_{0}}^{2}$.
点评 本题是难点为分析带电粒子的难点是分析带电粒子的运动情况,可通过画轨迹作速度图象分析什么时刻进入偏转电场的电子侧向最大与最小.


科目:高中物理 来源: 题型:解答题
 如图所示,竖直放置的两端封闭的玻璃管中注满清水,内有一个红蜡块能在水中匀速上浮.在红蜡块从玻璃管的下端匀速上浮的同时,使玻璃管以速度v水平向右匀速运动.已知蜡块匀速上升的速度大小为3cm/s,玻璃管水平运动的速度大小为4cm/s,则:
如图所示,竖直放置的两端封闭的玻璃管中注满清水,内有一个红蜡块能在水中匀速上浮.在红蜡块从玻璃管的下端匀速上浮的同时,使玻璃管以速度v水平向右匀速运动.已知蜡块匀速上升的速度大小为3cm/s,玻璃管水平运动的速度大小为4cm/s,则:查看答案和解析>>
科目:高中物理 来源: 题型:解答题
查看答案和解析>>
科目:高中物理 来源: 题型:多选题
| A. | 激光比普通光源的相干性好 | |
| B. | 紫光在水中的传播速度大于红光在水中的传播速度 | |
| C. | 在光的衍射实验中,出现明条纹的地方光子到达的概率较大 | |
| D. | 氘和氦3的核聚变反应方程式:${\;}_{1}^{2}$H+${\;}_{2}^{3}$He→${\;}_{2}^{4}$He+X,其中X是正电子 |
查看答案和解析>>
科目:高中物理 来源: 题型:解答题

| 次数 | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| S(m) | 4.5 | 3.9 | 3.0 | 2.1 | 1.5 | 0.9 | 0.3 |
| V(mL)90 | 90 | 84 | 72 | 62 | 52 | 40 | 23.5 |
| $\frac{s}{{V}^{2}}$ | 5.6×10-4 | 5.5×10-4 | 5.58×10-4 | 5.5×10-4 | 5.6×10-4 | 5.6×10-4 | 5.4×10-4 |
查看答案和解析>>
科目:高中物理 来源: 题型:解答题
 如图所示,带电平行金属板相距为2R,在两板间半径为R的圆形区域内有垂直纸面向里的匀强磁场,磁感应强度为B,两板及其左侧边缘连线均与磁场边界刚好相切.一质子(不计重力)沿两板间中心线O1O2从左侧O1点以某一速度射入,沿直线通过圆形磁场区域,然后恰好从极板边缘飞出,在极板间运动时间为t0.若仅撤去磁场,质子仍从O1点以相同速度射入,经$\frac{{t}_{0}}{2}$时间打到极板上.
如图所示,带电平行金属板相距为2R,在两板间半径为R的圆形区域内有垂直纸面向里的匀强磁场,磁感应强度为B,两板及其左侧边缘连线均与磁场边界刚好相切.一质子(不计重力)沿两板间中心线O1O2从左侧O1点以某一速度射入,沿直线通过圆形磁场区域,然后恰好从极板边缘飞出,在极板间运动时间为t0.若仅撤去磁场,质子仍从O1点以相同速度射入,经$\frac{{t}_{0}}{2}$时间打到极板上.查看答案和解析>>
科目:高中物理 来源: 题型:解答题
 如图,空间有一水平向右的有界匀强电场,上下宽度l=12cm,沿电场线上的A、B两点间的距离d=8cm,AB两点间的电势差UAB=160V.一带正电的粒子,电量q=5.0×10-10C,质量m=1.0×10-20kg,从电场的上边界R点沿电场的垂线RO飞入电场,初速度v0=3×106m/s.粒子从电场的下边界飞出电场后,经过无场区域进入水平界面为MN、PQ的匀强磁场区域,从磁场的PQ边界出来后刚好打在直线RO上离PQ边界L处的S点上,且电场的下边界到界面MN的距离以及两界面MN与PQ间的距离均为L.已知粒子进入界面MN时偏离直线RO的距离为24cm,粒子重力不计.求:
如图,空间有一水平向右的有界匀强电场,上下宽度l=12cm,沿电场线上的A、B两点间的距离d=8cm,AB两点间的电势差UAB=160V.一带正电的粒子,电量q=5.0×10-10C,质量m=1.0×10-20kg,从电场的上边界R点沿电场的垂线RO飞入电场,初速度v0=3×106m/s.粒子从电场的下边界飞出电场后,经过无场区域进入水平界面为MN、PQ的匀强磁场区域,从磁场的PQ边界出来后刚好打在直线RO上离PQ边界L处的S点上,且电场的下边界到界面MN的距离以及两界面MN与PQ间的距离均为L.已知粒子进入界面MN时偏离直线RO的距离为24cm,粒子重力不计.求:查看答案和解析>>
科目:高中物理 来源: 题型:多选题
| A. | 减小电源的频率 | |
| B. | 增大电源的频率 | |
| C. | 保持电源的频率不变,在线圈中加入铁芯 | |
| D. | 保持电源的频率不变,减少线圈的匝数 |
查看答案和解析>>
科目:高中物理 来源: 题型:选择题
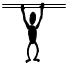 某同学在做引体向上时,两臂伸直对称吊在单杠上,两臂夹角为60°,已知该同学的体重为60kg,则两只手臂的拉力分别是( )(g取10m/s2)
某同学在做引体向上时,两臂伸直对称吊在单杠上,两臂夹角为60°,已知该同学的体重为60kg,则两只手臂的拉力分别是( )(g取10m/s2)| A. | 300N | B. | 200$\sqrt{3}$N | C. | 100N | D. | 600N |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com