
 ��ͼ��ʾΪ������Ÿ�Ӧ���ٴ�ԭ��ͼ������ͼ����������ͨ��������������ǿ�ų����䷽��ֱ�������ϣ���СΪB������Ϊd���������ײ��̶���һ������L1������L2��N�Ѿ�����Ȧ����Ȧ���ܵ���ΪR��������Ȧ��������Ϊm�����������˶�����������������Ϊf���������Գ��ٶ�v0����ų��������࣬��ʼ�Դ�СΪa�ĺ㶨���ٶȼ���ʻ��ų�������Ȧȫ������ų�������������ֱ���˶���ֱ����ȫ�뿪����������֪����Ȧ�ս���ų�����ȫ�����ų��Ĺ����У�������ǣ���������ܹ�ΪW������Ȧ��ǰ����ų�������غϿ�ʼ��ʱ����
��ͼ��ʾΪ������Ÿ�Ӧ���ٴ�ԭ��ͼ������ͼ����������ͨ��������������ǿ�ų����䷽��ֱ�������ϣ���СΪB������Ϊd���������ײ��̶���һ������L1������L2��N�Ѿ�����Ȧ����Ȧ���ܵ���ΪR��������Ȧ��������Ϊm�����������˶�����������������Ϊf���������Գ��ٶ�v0����ų��������࣬��ʼ�Դ�СΪa�ĺ㶨���ٶȼ���ʻ��ų�������Ȧȫ������ų�������������ֱ���˶���ֱ����ȫ�뿪����������֪����Ȧ�ս���ų�����ȫ�����ų��Ĺ����У�������ǣ���������ܹ�ΪW������Ȧ��ǰ����ų�������غϿ�ʼ��ʱ�������� ��1�����ݵ�Ÿ�Ӧ֪ʶ��ð�����������ţ�ٵڶ��������ǣ�����Ĵ�С�����ɹ��ʹ�ʽ��P=Fv��⼴�ɣ�
��2�������˶���ʽ�����˶�ѧ��ʽ�������ֱ���˶���ʱ�䣬�ɽ���������������˶������Ľ����ȣ��ٽ�������غ���⣮
��� �⣺��1����Ȧ����ų�ʱ�ٶ�Ϊvʱ��Ӧ�綯�ƣ�E=BL2v
��ŷķ���ɵã�I=$\frac{E}{R}$
����Ȧ�ܵ��İ�������F��=BIL2=$\frac{{B}^{2}{L}_{2}^{2}v}{R}$
����ţ�ٵڶ����ɵã�F-F��-f=ma
��ã�F=f+ma+$\frac{{B}^{2}{L}_{2}^{2}v}{R}$
����Ϊ��Ȧ���ȼ����˶������У�v=v0-at
��Ϲ��ʹ�ʽ��P=Fv
��ã�P=��f+ma+$\frac{{B}^{2}{L}_{2}^{2}v}{R}$����v0-at��
��2������Ȧ�Ժ㶨�ٶ�v���ų������˶�ѧ��ʽ��v2-${v}_{0}^{2}$=2aL1
�ã�v=$\sqrt{{v}_{0}^{2}-2a{L}_{1}}$
�˶�ʱ��Ϊ��t=$\frac{{L}_{1}}{v}$
�����ĸ�Ӧ�綯��Ϊ��E=BL2v
��Ӧ����Ϊ��I=$\frac{E}{R}$
�ɽ������ɵã����������� Q��=I2Rt
�������غ㶨�ɵã�W=$\frac{1}{2}$mv2+f��d+L1��+Q��+Q��
��ã�Q��=W-$\frac{1}{2}$m��${v}_{0}^{2}$-2aL1��-f��d+L1��-$\frac{{B}^{2}{L}_{2}^{2}{L}_{1}\sqrt{{v}_{0}^{2}-2a{L}_{1}}}{R}$
�𣺣�1��ǣ�����Ĺ�����ʱ��仯�Ĺ�ϵʽΪP=��f+ma+$\frac{{B}^{2}{L}_{2}^{2}v}{R}$����v0-at����
��2����Ȧ����ų������У���Ȧ�в����Ľ�����ΪW-$\frac{1}{2}$m��${v}_{0}^{2}$-2aL1��-f��d+L1��-$\frac{{B}^{2}{L}_{2}^{2}{L}_{1}\sqrt{{v}_{0}^{2}-2a{L}_{1}}}{R}$��
���� ��������ѧ��ѧ���ϵ��ۺ��⣬�������������ǹؼ�����Ҫ��ȷ�������������ת���ģ������˶����̺��������ù�ʽ��⼴�ɣ�



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ���������� ��Դ�� ���ͣ���ѡ��
| A�� | 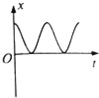 | B�� | 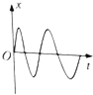 | C�� | 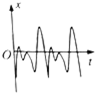 | D�� | 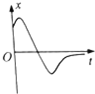 |
�鿴�𰸺ͽ���>>
��Ŀ���������� ��Դ�� ���ͣ���ѡ��
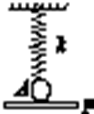 ��ͼ��ʾ������ϵ��Ϊk���ᵯ���¶�ϵһ������Ϊm��С��A��С��ˮƽ����P��סʹ���ɳ���ǡΪ��Ȼ���ȣ�С���뵲�岻ճ������Ȼ��ʹ����P�Ժ㶨�ļ��ٶ�a��a��g����ʼ��ֱ�������ȼ���ֱ���˶���������
��ͼ��ʾ������ϵ��Ϊk���ᵯ���¶�ϵһ������Ϊm��С��A��С��ˮƽ����P��סʹ���ɳ���ǡΪ��Ȼ���ȣ�С���뵲�岻ճ������Ȼ��ʹ����P�Ժ㶨�ļ��ٶ�a��a��g����ʼ��ֱ�������ȼ���ֱ���˶���������| A�� | С�����뵲������ʱ��Ϊt=$\sqrt{\frac{ka}{2m��g-a��}}$ | |
| B�� | С�����뵲������ʱ��Ϊt=$\sqrt{\frac{2m��g-a��}{ka}}$ | |
| C�� | С��ӿ�ʼ�˶�ֱ����͵�Ĺ����У�С���ٶ����ʱ���ɵ��쳤��x=$\frac{mg}{k}$ | |
| D�� | С��ӿ�ʼ�˶�ֱ����͵�Ĺ����У�С���ٶ����ʱ���ɵ��쳤��x=$\frac{m��g-a��}{k}$ |
�鿴�𰸺ͽ���>>
��Ŀ���������� ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ���������� ��Դ�� ���ͣ������
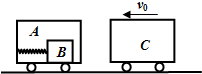 ��ͼ��ʾ������Ϊ2M��С��A��ֹ�ڹ⻬ˮƽ�����ϣ�����Ϊ3M������B������A�������ڣ�B������ᵯ����A�����ӣ����ɾ���ϵ��Ϊk��ˮƽ������ԭ����С������⻬������ΪM��С��C���ٶ�v0��С��A����ȥ��������С��A��ײ��������A��ճ��������������Bʼ�ղ��복������ײ����֮����˶������е��ɵ��������̳���֮������ɵ������ܱ���ʽΪEp=$\frac{1}{2}$kx2��xΪ�����α�������
��ͼ��ʾ������Ϊ2M��С��A��ֹ�ڹ⻬ˮƽ�����ϣ�����Ϊ3M������B������A�������ڣ�B������ᵯ����A�����ӣ����ɾ���ϵ��Ϊk��ˮƽ������ԭ����С������⻬������ΪM��С��C���ٶ�v0��С��A����ȥ��������С��A��ײ��������A��ճ��������������Bʼ�ղ��복������ײ����֮����˶������е��ɵ��������̳���֮������ɵ������ܱ���ʽΪEp=$\frac{1}{2}$kx2��xΪ�����α��������鿴�𰸺ͽ���>>
��Ŀ���������� ��Դ�� ���ͣ�ѡ����
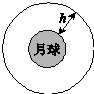 �ҹ��������ɡ���ʮ���롰�칬���Խӡ����϶�Я�����á����������칤�̣�ij���찮������������á��ؼҵ����룺��ͼ��ʾ����Я�������á��ķ���ϵͳ��������淢�䵽h�߶ȵĹ���ϣ����ڸù����������Բ���˶��ķɴ��Խӣ�Ȼ���ɷɴ��͡����á����ص����衰���á�����Ϊm������뾶ΪR��������������ٶ�Ϊg����������Ϊ�������棬�����á���h�߶ȵ��������ܿɱ�ʾΪEp=$\frac{GMmh}{R��R+h��}$������GΪ����������MΪ�����������������������ת���ӿ�ʼ���䵽�Խ������Ҫ�ԡ����á����Ĺ�Ϊ��������
�ҹ��������ɡ���ʮ���롰�칬���Խӡ����϶�Я�����á����������칤�̣�ij���찮������������á��ؼҵ����룺��ͼ��ʾ����Я�������á��ķ���ϵͳ��������淢�䵽h�߶ȵĹ���ϣ����ڸù����������Բ���˶��ķɴ��Խӣ�Ȼ���ɷɴ��͡����á����ص����衰���á�����Ϊm������뾶ΪR��������������ٶ�Ϊg����������Ϊ�������棬�����á���h�߶ȵ��������ܿɱ�ʾΪEp=$\frac{GMmh}{R��R+h��}$������GΪ����������MΪ�����������������������ת���ӿ�ʼ���䵽�Խ������Ҫ�ԡ����á����Ĺ�Ϊ��������| A�� | $\frac{m{g}_{��}R}{R+h}$��h+2R�� | B�� | $\frac{m{g}_{��}R}{R+h}$��h+$\sqrt{2}$R�� | C�� | $\frac{m{g}_{��}R}{R+h}$��h+$\frac{\sqrt{2}}{2}$R�� | D�� | $\frac{m{g}_{��}R}{R+h}$��h+$\frac{1}{2}$R�� |
�鿴�𰸺ͽ���>>
��Ŀ���������� ��Դ�� ���ͣ������
 ��ͼ��ʾ��һ������Ϊ4t���������پ���һ�뾶Ϊ50m�����ţ���g=10m/s2��
��ͼ��ʾ��һ������Ϊ4t���������پ���һ�뾶Ϊ50m�����ţ���g=10m/s2���鿴�𰸺ͽ���>>
��Ŀ���������� ��Դ�� ���ͣ������
 һ����Ϊl�IJ����쳤������ϸ���¶�ϵһ����Ϊm����Ϊ�ʵ��С����ͼ��ʾ��ˮƽ����������Բ���˶���ϸ�ߺ���ֱ����ļнǦ�=53�㣬��ȡsin37��=0.60��cos37��=0.80��
һ����Ϊl�IJ����쳤������ϸ���¶�ϵһ����Ϊm����Ϊ�ʵ��С����ͼ��ʾ��ˮƽ����������Բ���˶���ϸ�ߺ���ֱ����ļнǦ�=53�㣬��ȡsin37��=0.60��cos37��=0.80���鿴�𰸺ͽ���>>
��Ŀ���������� ��Դ�� ���ͣ���ѡ��
| A�� | ���ܹ�Դ��۲����Ƿ��������˶����۲��߹۲쵽�Ĺ����Dz���� | |
| B�� | ˮ���ϵ���Ĥ���ֲ�ɫ�ǹ�ĸ������� | |
| C�� | �ڹ��ά���ڴ���ͼ�������ù��ɫɢ���� | |
| D�� | ��Դ��ֹ�Ĺ۲����˶����۲��߽��յ���Ƶ��С����Դ��Ƶ�� | |
| E�� | δ��������������������Ϊ���������ϳ����������������� |
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com