
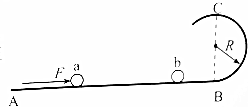
 如图所示,ABC为竖直平面内的光滑轨道,AB部分水平,BC部分是半径为R的圆弧轨道.小球a、b均静止在水平轨道上,两者相隔一定距离,两小球的质量分别为ma=2m、mb=m.现对a施加一水平恒力F使其从静止开始运动,作用时间t后撤去F,之后a与b发生对心弹性正碰,要使碰后两球均能通过圆弧轨道的最高点C,求F至少应为多大?
如图所示,ABC为竖直平面内的光滑轨道,AB部分水平,BC部分是半径为R的圆弧轨道.小球a、b均静止在水平轨道上,两者相隔一定距离,两小球的质量分别为ma=2m、mb=m.现对a施加一水平恒力F使其从静止开始运动,作用时间t后撤去F,之后a与b发生对心弹性正碰,要使碰后两球均能通过圆弧轨道的最高点C,求F至少应为多大? 分析 要使小球通过最高点C,在C点的向心力最小应等于重力,求出最高点的临界速度,再由机械能守恒定律求出在B点的速度,结合弹性碰撞动量守恒和机械能守恒求出碰撞前a球的最小速度,最后由动量定理求F的最小值.
解答 解:对于任意一个小球恰好通过C点时,有 m′g=m′$\frac{{v}_{C}^{2}}{R}$,得 vC=$\sqrt{gR}$
小球从最低点B到最高点C的过程,由机械能守恒定律得:2m′gR+$\frac{1}{2}m{v}_{C}^{2}$=$\frac{1}{2}m{v}_{B}^{2}$,解得 vB=$\sqrt{5gR}$
设a与b碰撞前a的速度为v0.取向右为正方向,根据动量守恒定律和机械能守恒定律得:
mav0=mava+mbvb;
$\frac{1}{2}{m}_{a}{v}_{0}^{2}$=$\frac{1}{2}{m}_{a}{v}_{a}^{2}$+$\frac{1}{2}{m}_{b}{v}_{b}^{2}$
又 ma=2m、mb=m
联立解得 va=$\frac{1}{3}{v}_{0}$,vb=$\frac{4}{3}{v}_{0}$
所以要使碰后两球均能通过圆弧轨道的最高点C,只要满足条件:va=$\frac{1}{3}{v}_{0}$≥$\sqrt{5gR}$,即可.
则v0的最小值为 v0=3$\sqrt{5gR}$
对碰撞前a的运动过程,由动量定理得
Ft=mav0;
解得 F的最小值 F=$\frac{6m\sqrt{5gR}}{t}$
答:F至少应为$\frac{6m\sqrt{5gR}}{t}$.
点评 解决本题的关键要把握每个过程和状态的物理规律,明确小球恰好通过最高点的临界条件:重力等于向心力,知道弹性碰撞遵守两大守恒:动量守恒和机械能守恒.


 金版课堂课时训练系列答案
金版课堂课时训练系列答案 单元全能练考卷系列答案
单元全能练考卷系列答案 新黄冈兵法密卷系列答案
新黄冈兵法密卷系列答案科目:高中物理 来源: 题型:填空题

查看答案和解析>>
科目:高中物理 来源: 题型:多选题
 如图所示,平行金属板中的带电质点P处于静止状态,不考虑电流表和电压对电路的影响,当滑动变阻器R4滑片向b端移动时( )
如图所示,平行金属板中的带电质点P处于静止状态,不考虑电流表和电压对电路的影响,当滑动变阻器R4滑片向b端移动时( )| A. | 电流表读数增大 | B. | 电压表读数减小 | ||
| C. | R3上消耗的电功率增大 | D. | 质点P将向下运动 |
查看答案和解析>>
科目:高中物理 来源: 题型:选择题
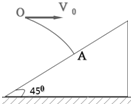 如图所示,从O点以10m/s水平初速度v0抛出的物体,飞行一段时间后,垂直地撞在倾角为45°的斜面上的A点. 则物体完成这段飞行的时间是 (g=10m/s2)( )
如图所示,从O点以10m/s水平初速度v0抛出的物体,飞行一段时间后,垂直地撞在倾角为45°的斜面上的A点. 则物体完成这段飞行的时间是 (g=10m/s2)( )| A. | 1s | B. | 1.5s | C. | 2s | D. | 1.4s |
查看答案和解析>>
科目:高中物理 来源: 题型:多选题
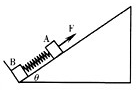 如图所示,倾角为θ足够长的光滑斜面下端固定一挡板,质量均为m的两物块用轻质弹簧连接静止在光滑斜面上,现用平行斜面向上的恒力F作用在物块A上,使A开始向上运动,下列说法正确的是( )
如图所示,倾角为θ足够长的光滑斜面下端固定一挡板,质量均为m的两物块用轻质弹簧连接静止在光滑斜面上,现用平行斜面向上的恒力F作用在物块A上,使A开始向上运动,下列说法正确的是( )| A. | 若F<2mgsinθ,物块B一定不能离开挡板 | |
| B. | 若F=2mgsinθ,物块B一定能离开挡板 | |
| C. | 若F>2mgsinθ,弹簧第一次到达最长时,B的加速度一定大于A的加速度 | |
| D. | 若F>2mgsinθ,拉力F做的功总等于A机械能的增量与弹簧弹性势能增量之和 |
查看答案和解析>>
科目:高中物理 来源: 题型:选择题
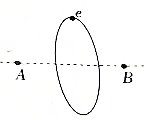 在一条水平直线上相距2a的A、B两点,固定有等量同种电荷,电荷量为q,一电子好在直线AB的中垂面上半径为a的匀速圆周运动,如图所示,已知电子的电荷量为e,重力不计,则( )
在一条水平直线上相距2a的A、B两点,固定有等量同种电荷,电荷量为q,一电子好在直线AB的中垂面上半径为a的匀速圆周运动,如图所示,已知电子的电荷量为e,重力不计,则( )| A. | A,B两点的电荷均带负电 | |
| B. | 电子轨道所在位置的场强处处相同 | |
| C. | 若将A、B两点的电荷缓慢向两侧移动,电子的轨道半径减小 | |
| D. | 电子做圆周运动的角速度为$\sqrt{\frac{\sqrt{2}kqe}{2m{a}^{3}}}$ |
查看答案和解析>>
科目:高中物理 来源: 题型:解答题
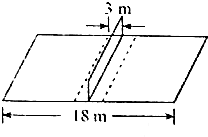 中国女排2011年重夺亚洲冠军,从而昂首入围世界杯,排球场总长为18m,设网高度为2.25m,如图所示,假设从日本队飞来一球,刚好在3m线正上方被王一梅后排强攻击回,假设排球被击回的初速度方向是水平的,将排球视为质点.且排球在飞行过程中所受空气从力和浮力均不计.取g=10m/s2.
中国女排2011年重夺亚洲冠军,从而昂首入围世界杯,排球场总长为18m,设网高度为2.25m,如图所示,假设从日本队飞来一球,刚好在3m线正上方被王一梅后排强攻击回,假设排球被击回的初速度方向是水平的,将排球视为质点.且排球在飞行过程中所受空气从力和浮力均不计.取g=10m/s2.查看答案和解析>>
科目:高中物理 来源: 题型:解答题
 小张同学采用如图1所示的实验装置做“研究平抛运动”的实验.
小张同学采用如图1所示的实验装置做“研究平抛运动”的实验.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com