
 如图所示,一带电粒子从直角坐标系中y轴上的A点沿直线穿过速度选择器,一段时间后进入一垂直于纸面向里的圆形匀强磁场区域(图中未画出磁场区域),粒子飞出磁场后立即从m板边缘C点平行于板面进入匀强电场,偏转后恰好从n板边缘(x轴上的D点)与x轴正方向成30°角穿过.已知带电粒子的质量为m,电量大小为q,重力不计,A点坐标(0,-b),∠COD=45°,所有匀强磁场和匀强电场的强度均分别为B和E,试求:
如图所示,一带电粒子从直角坐标系中y轴上的A点沿直线穿过速度选择器,一段时间后进入一垂直于纸面向里的圆形匀强磁场区域(图中未画出磁场区域),粒子飞出磁场后立即从m板边缘C点平行于板面进入匀强电场,偏转后恰好从n板边缘(x轴上的D点)与x轴正方向成30°角穿过.已知带电粒子的质量为m,电量大小为q,重力不计,A点坐标(0,-b),∠COD=45°,所有匀强磁场和匀强电场的强度均分别为B和E,试求:分析 (1)根据粒子在电场中及磁场中的运动可得出粒子及极板的带电量;
(2)根据洛仑兹力充当向心力可求得粒子的半径,要使粒子能从磁场穿出,磁场区域应包含粒子的整个圆,故最小磁场的直径应为$\sqrt{2}$R;
(3)根据几何关系可明确平行板的间距,由竖直方向的匀加速直线运动可求得在电容中的时间;磁场中恰好经过四分之一周期,由周期公式求得时间;粒子在速度选择器中做匀速直线运动;由速度公式可求得时间.
解答 解:(1)带电粒子在磁场中向右偏转,根据左手定则可知,粒子带负电;
粒子在极板间向下偏转,故m板带负电;
因粒子穿过速度选择器,则在速度选择器中有:
Bqv0=Eq
解得:离开速度选择器的速度为:v=$\frac{E}{B}$;
经过磁场时速度大小不变;在电场中做类平抛运动;
穿出时的速度v=$\frac{{v}_{0}}{cos30°}$=$\frac{2\sqrt{3}E}{3B}$;
(2)由洛仑兹力充当向心力可知:
带电粒子在磁场中的半径R=$\frac{mv}{Bq}$=$\frac{mE}{{B}^{2}q}$
由几何关系可知,粒子在磁场中应经历四分之一个圆周;
圆形磁场的最小半径为:r=$\frac{\sqrt{2}}{2}R$=$\sqrt{2}$R=$\frac{1}{2}$$\frac{\sqrt{2}mE}{{B}^{2}q}$;
则最小面积S=πr2=$\frac{π{m}^{2}{E}^{2}}{{2B}^{4}{q}^{2}}$
(3)因∠COD=45°;由几何关系可知,OC一定是磁场的直径;
则OC的长度为$\sqrt{2}$R;O′C=$\frac{\sqrt{2}}{2}OC$=R=$\frac{mE}{{B}^{2}q}$;
则在竖直方向有:R=$\frac{1}{2}$at2=$\frac{1}{2}×\frac{Eq}{m}{t}^{2}$
解得:t=$\frac{\sqrt{2}m}{Bq}$;
在磁场中的时间t2=$\frac{T}{4}$=$\frac{2πm}{Bq}×\frac{1}{4}$=$\frac{πm}{2Bq}$;
粒子在速度选择器中的时间t3=$\frac{d}{v}$=$\frac{Bb}{E}$
总时间t总=t+t2+t3=$\frac{\sqrt{2}m}{Bq}$+$\frac{πm}{2Bq}$+$\frac{Bb}{E}$
答:(1)m极板所带电荷的电性为负电;粒子经过D点时的速度大小$\frac{2\sqrt{3}E}{3B}$;
(2)圆形磁场区域的最小面积$\frac{π{m}^{2}{E}^{2}}{{2B}^{4}{q}^{2}}$
(3)粒子从A到D所经历的时间$\frac{\sqrt{2}m}{Bq}$+$\frac{πm}{2Bq}$+$\frac{Bb}{E}$.
点评 本题考查带电粒子在电场和磁场中的运动,要注意正确理解几何关系,用好不同场中的物理规律求解.


科目:高中物理 来源: 题型:多选题
| A. | 火星表面重力加速度的数值比地球表面的小 | |
| B. | 火星公转的周期比地球的大 | |
| C. | 火星公转的线速度比地球的大 | |
| D. | 火星公转的向心加速度比地球的大 |
查看答案和解析>>
科目:高中物理 来源: 题型:填空题
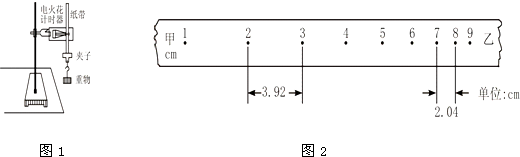
查看答案和解析>>
科目:高中物理 来源: 题型:解答题
 如图所示,质量为m1的木块A放在光滑水平面上,A上放置一质量为m2的另一木块B,A、B间的摩擦因数为μ.用水平力F1拉m1,使两木块都能一起运动,求:
如图所示,质量为m1的木块A放在光滑水平面上,A上放置一质量为m2的另一木块B,A、B间的摩擦因数为μ.用水平力F1拉m1,使两木块都能一起运动,求:查看答案和解析>>
科目:高中物理 来源: 题型:解答题
 如图所示,水平放置的平行金属导轨宽度为d=1m,导轨间接有一个阻值为R=2Ω的灯泡,一质量为m=1Kg的金属棒跨接在导轨之上,其电阻为r=1Ω,且和导轨始终接触良好,整个装置放在磁感应强度为B=2T的匀强磁场中,磁场方向垂直导轨平面向下,现对金属棒施加一水平向右的拉力F,使金属棒从静止开始向右运动.求:
如图所示,水平放置的平行金属导轨宽度为d=1m,导轨间接有一个阻值为R=2Ω的灯泡,一质量为m=1Kg的金属棒跨接在导轨之上,其电阻为r=1Ω,且和导轨始终接触良好,整个装置放在磁感应强度为B=2T的匀强磁场中,磁场方向垂直导轨平面向下,现对金属棒施加一水平向右的拉力F,使金属棒从静止开始向右运动.求:查看答案和解析>>
科目:高中物理 来源: 题型:解答题
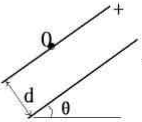 如图所示,两平行金属板的极板间距为d,极板面与水平面成θ角,左极板中心开有一小孔O,当两极板间加上一定的电压后,一质量为m、电荷量为q的带电粒子以不同的速度从O点水平射入平射入极板间后,能从O孔反射出来,小球在电场中运动时间最长不超过多少?
如图所示,两平行金属板的极板间距为d,极板面与水平面成θ角,左极板中心开有一小孔O,当两极板间加上一定的电压后,一质量为m、电荷量为q的带电粒子以不同的速度从O点水平射入平射入极板间后,能从O孔反射出来,小球在电场中运动时间最长不超过多少?查看答案和解析>>
科目:高中物理 来源: 题型:选择题
| A. | mgh-$\frac{1}{2}$mv2-$\frac{1}{2}$mv02 | B. | -$\frac{1}{2}$mv2-$\frac{1}{2}$mv02-mgh | ||
| C. | mgh+$\frac{1}{2}$mv02-$\frac{1}{2}$mv2 | D. | $\frac{1}{2}$mv02-$\frac{1}{2}$mv2-mgh |
查看答案和解析>>
科目:高中物理 来源: 题型:解答题
查看答案和解析>>
科目:高中物理 来源: 题型:解答题

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com