
分析 (1)绕地球表面附近做圆周运动的人造卫星,可认为其轨道半径是地球的半径R,万有引力等于重力,可利用万有引力提供它做圆周运动的向心力来进行求解.
(2)根据万有引力等于重力求解某星球表面的重力加速度g′.
解答 解:(1)因为卫星绕地球表面附近做圆周运动,所以可认为其轨道半径是地球的半径R,万有引力等于重力,
由万有引力提供卫星做圆周运动的向心力得:
mg=m$\frac{{v}^{2}}{R}$
得第一宇宙速度:v=$\sqrt{gR}$
(2)在星球表面,根据万有引力等于重力得:
地球表面:$G\frac{Mm}{{R}^{2}}=mg$
某星球表面:$G\frac{M′m}{{R′}^{2}}=mg′$,
根据某星球的质量是地球的8倍,半径是地球的2倍,
解得:g′=2g
答:(1)地球的第一宇宙速度v为$\sqrt{gR}$;
(2)某星球表面的重力加速度g′为2g.
点评 万有引力提供卫星做圆周运动的向心力是解决这类题目的突破口,知道在星球表面万有引力等于重力,难度不大,属于基础题.


 学期复习一本通学习总动员期末加暑假延边人民出版社系列答案
学期复习一本通学习总动员期末加暑假延边人民出版社系列答案 芒果教辅暑假天地重庆出版社系列答案
芒果教辅暑假天地重庆出版社系列答案科目:高中物理 来源: 题型:解答题
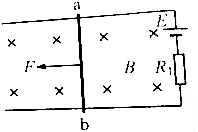 如图所示,在竖直向下的匀强磁场中,水平放置两根间距L=0.2m的平行光滑金属直导轨,一端接有电动势E=6V的理想电源和R1=14Ω的电阻,阻值R2=1Ω的金属棒ab与导轨接触良好,在水平拉力F=0.2N的作用下,金属棒ab保持静止状态(其余电阻不计).求:
如图所示,在竖直向下的匀强磁场中,水平放置两根间距L=0.2m的平行光滑金属直导轨,一端接有电动势E=6V的理想电源和R1=14Ω的电阻,阻值R2=1Ω的金属棒ab与导轨接触良好,在水平拉力F=0.2N的作用下,金属棒ab保持静止状态(其余电阻不计).求:查看答案和解析>>
科目:高中物理 来源: 题型:解答题
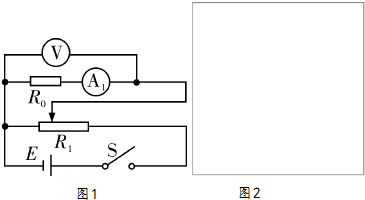
查看答案和解析>>
科目:高中物理 来源: 题型:解答题
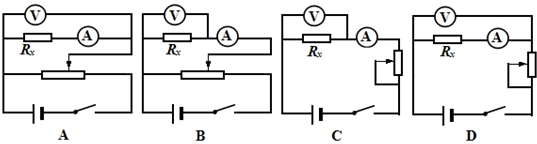
查看答案和解析>>
科目:高中物理 来源: 题型:多选题
| A. | 物体受到的向心力是4N | B. | 物体的线速度大小是4m/s | ||
| C. | 物体的加速度大小是4m/s2 | D. | 物体运动的周期为2π |
查看答案和解析>>
科目:高中物理 来源: 题型:多选题
| A. | 它是人造地球卫星绕地球飞行的最小速度 | |
| B. | 它是近地圆形轨道上人造地球卫星的运行速度 | |
| C. | 它是能使卫星进入近地圆形轨道的最小发射速度 | |
| D. | 物体摆脱地球引力所必须具有的速度 |
查看答案和解析>>
科目:高中物理 来源: 题型:解答题
查看答案和解析>>
科目:高中物理 来源: 题型:解答题
 猎豹是目前世界上在陆地奔跑速度最快的动物,但不能维持长时间高速奔跑,否则会因身体过热而危及生命.猎豹在一次追击猎物时(如图),经4s速度由静止达到最大,然后匀速运动保持了4s仍没追上猎物,为保护自己它放弃了这次行动,以3m/s2的加速度减速,经10s停下,设此次追捕猎豹始终沿直线运动.
猎豹是目前世界上在陆地奔跑速度最快的动物,但不能维持长时间高速奔跑,否则会因身体过热而危及生命.猎豹在一次追击猎物时(如图),经4s速度由静止达到最大,然后匀速运动保持了4s仍没追上猎物,为保护自己它放弃了这次行动,以3m/s2的加速度减速,经10s停下,设此次追捕猎豹始终沿直线运动.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com