
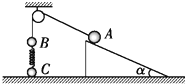
 如图所示,A,B两小球由绕过轻质定滑轮的细线相连,A放在固定的光滑斜面上,B、C两小球在竖直方向上通过劲度系数为k的轻质弹簧相连,C放在水平地面上.现用手控制住A,并使细线刚刚拉直但无拉力作用,并保证定滑轮左侧细线竖直,右侧细线与斜面平行.已知B、C的质量均为m,重力加速度为g,细线与滑轮之间的摩擦不计,开始时整个系统处于静止状态.已知斜面倾角α=30°.
如图所示,A,B两小球由绕过轻质定滑轮的细线相连,A放在固定的光滑斜面上,B、C两小球在竖直方向上通过劲度系数为k的轻质弹簧相连,C放在水平地面上.现用手控制住A,并使细线刚刚拉直但无拉力作用,并保证定滑轮左侧细线竖直,右侧细线与斜面平行.已知B、C的质量均为m,重力加速度为g,细线与滑轮之间的摩擦不计,开始时整个系统处于静止状态.已知斜面倾角α=30°.分析 (1)C球刚离开地面时,弹簧的弹力等于C的重力,根据牛顿第二定律知B的加速度为零,B、C加速度相同,分别对B、A受力分析,列出平衡方程,可以求出A的质量,对B、C组成的系统由动能定理可以求出最大速度.
(2)A下滑至位移最大时,速度为0,对系统根据机械能守恒列式,A减少的重力势能等于B增加的势能
(3)判断物体C能否离开地面,取决于A的质量是否大于临界值,经判断能离开地面,再对系统运用机械能守恒即可求解
解答 解:(1)当A所受合力为零时,速度最大,此时:aA=aB=aC=0,
此时C刚离开地面时,由平衡条件得:
对C:kx2=mg,
对B:T-kx2-mg=0,
对A:M1gsin30°-T=0,
解得:M1=4m;
开始时系统静止,且线上无拉力,
对B有:kx1=mg,
解得:x1=x2=$\frac{mg}{k}$,
则从释放A至C刚离开地面过程中,弹性势能变化量为零,此过程中由机械能守恒得:
M1g(x1+x2)sin30°-mg(x1+x2)=$\frac{1}{2}$(M1+m)v2-0,解得:v=2g$\sqrt{\frac{m}{5k}}$;
(2)根据机械能守恒守恒定律${M}_{2}^{\;}g({x}_{1}^{\;}+{x}_{2}^{\;})sin30°=mg({x}_{1}^{\;}+{x}_{2}^{\;})$
解得:${M}_{2}^{\;}=2m$
(3)当$2m<{M}_{A}^{\;}=3m<4m$,C能离开地面
根据机械能守恒定律有:
${M}_{A}^{\;}g({x}_{1}^{\;}+{x}_{2}^{\;})sin30°-mg({x}_{1}^{\;}+{x}_{2}^{\;})$=$\frac{1}{2}({M}_{A}^{\;}+m){v}_{\;}^{2}$
解得:$v=g\sqrt{\frac{m}{2k}}$
答:(1)若释放A后,A沿斜面下滑至速度最大时C恰好要离开地面,A的质量${M}_{1}^{\;}$为4m和A获得的最大速度${v}_{m}^{\;}$为$2g\sqrt{\frac{m}{5k}}$;
(2)若释放A后,A沿斜面下滑至位移最大时C恰好要离开地面,A的质量${M}_{2}^{\;}$为2m;
(3)若A的质量MA=3m,释放A后,C能离开地面,C刚要离开地面时A、B的速度大小$g\sqrt{\frac{m}{2k}}$
点评 本题难度中等,根据各物体的受力判断运动的临界点是关键,系统在只有重力或弹力做功的情况下机械能守恒,物体所受合外力最大时加速度最大,注意A刚要离开地面时,弹簧的伸长量和刚开始的压缩量相同,所以弹性势能的变化量是0.


 第1卷单元月考期中期末系列答案
第1卷单元月考期中期末系列答案科目:高中物理 来源: 题型:选择题
| A. | A1:A2=1:3,T1:T2=1:2 | B. | A1:A2=1:3,T1:T2=2:1 | ||
| C. | A1:A2=3:1,T1:T2=1:2 | D. | A1:A2=3:1,T1:T2=2:1 |
查看答案和解析>>
科目:高中物理 来源: 题型:选择题
 汽车在行驶过程中对地面的压力过小是不安全的.有一辆质量为1600kg的小汽车驶上圆弧半径为50m的拱桥,g取10m/s2,则( )
汽车在行驶过程中对地面的压力过小是不安全的.有一辆质量为1600kg的小汽车驶上圆弧半径为50m的拱桥,g取10m/s2,则( )| A. | 若汽车以5 m/s的速度通过桥顶,对桥顶的压力为800 N | |
| B. | 若汽车以20 m/s的速度通过桥顶,恰好对桥顶没有压力 | |
| C. | 若汽车过桥的速度一定,拱桥半径越小,汽车越安全 | |
| D. | 若汽车过桥的速度一定,拱桥半径越大,汽车越安全 |
查看答案和解析>>
科目:高中物理 来源: 题型:解答题
 如图所示,一质量为m=3kg、初速度为5m/s的小滑块(可视为质点),向右滑上一质量为M=2kg的静止在水平面上足够长的滑板,m、M间动摩擦因数为μ1=0.2,滑板与水平面间的动摩擦因数为μ2=0.1,(设最大静摩擦力等于滑动摩擦力).
如图所示,一质量为m=3kg、初速度为5m/s的小滑块(可视为质点),向右滑上一质量为M=2kg的静止在水平面上足够长的滑板,m、M间动摩擦因数为μ1=0.2,滑板与水平面间的动摩擦因数为μ2=0.1,(设最大静摩擦力等于滑动摩擦力).查看答案和解析>>
科目:高中物理 来源: 题型:实验题
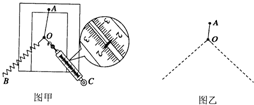 如图甲所示是“探究求共点力合力的方法”
如图甲所示是“探究求共点力合力的方法”查看答案和解析>>
科目:高中物理 来源: 题型:选择题
| A. | 在四分之一个周期内,物体通过的路程一定为振幅的1倍 | |
| B. | 在半个周期内,物体通过的路程不一定为振幅的2倍 | |
| C. | 在四分之三个周期内,物体通过的路程一定为振幅的3倍 | |
| D. | 在一个周期内,物体通过的路程一定为振幅的4倍 |
查看答案和解析>>
科目:高中物理 来源: 题型:多选题
| A. | β衰变所释放的电子是原子核外的电子电离形成的 | |
| B. | 普朗克为了解释黑体辐射现象,第一次提出了能量量子化理论 | |
| C. | 爱因斯坦为了解释光电效应的规律,提出了光子说 | |
| D. | 玻尔将量子观念引入原子领域,其理论能够解释氢原子光谱的特征 | |
| E. | 增大环境的压强或升高温度,都可使放射性物质的半衰期减小 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com