
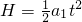
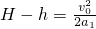



科目:高中物理 来源: 题型:解答题
查看答案和解析>>
科目:高中物理 来源: 题型:解答题
 如图,在水平雪地上,质量为M=25kg的小榕,坐在质量为,m=5kg的雪橇上,小岱用与水平方向成37°向上的拉力拉雪橇,拉力大小为F=100N,雪橇与地面间的动摩擦因数为μ=0.25,(sin37°=0.6,cos37°=0.8,g=10m/s2)
如图,在水平雪地上,质量为M=25kg的小榕,坐在质量为,m=5kg的雪橇上,小岱用与水平方向成37°向上的拉力拉雪橇,拉力大小为F=100N,雪橇与地面间的动摩擦因数为μ=0.25,(sin37°=0.6,cos37°=0.8,g=10m/s2)查看答案和解析>>
科目:高中物理 来源: 题型:单选题
查看答案和解析>>
科目:高中物理 来源: 题型:单选题
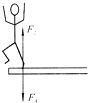 如图所示,运动员站在水平跳板上,图中F1表示人对跳板的压力,F2表示跳板对人的支持力,则下列说法中正确的是
如图所示,运动员站在水平跳板上,图中F1表示人对跳板的压力,F2表示跳板对人的支持力,则下列说法中正确的是查看答案和解析>>
科目:高中物理 来源: 题型:填空题

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com